
Question Number 188033 by Michaelfaraday last updated on 25/Feb/23
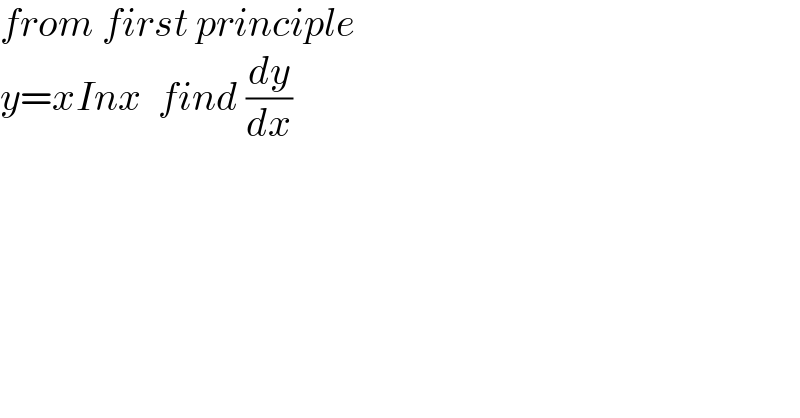
$${from}\:{first}\:{principle} \\ $$$${y}={xInx}\:\:{find}\:\frac{{dy}}{{dx}} \\ $$
Answered by a.lgnaoui last updated on 25/Feb/23
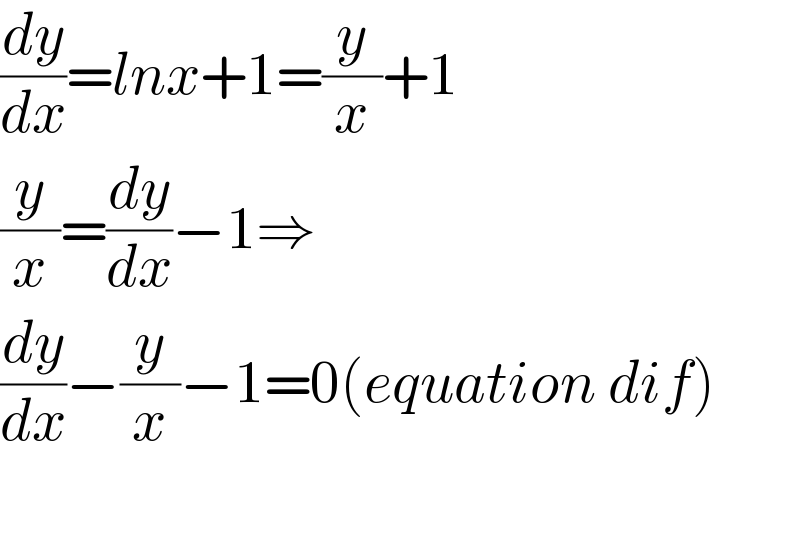
$$\frac{{dy}}{{dx}}={lnx}+\mathrm{1}=\frac{{y}}{{x}}+\mathrm{1} \\ $$$$\frac{{y}}{{x}}=\frac{{dy}}{{dx}}−\mathrm{1}\Rightarrow \\ $$$$\frac{{dy}}{{dx}}−\frac{{y}}{{x}}−\mathrm{1}=\mathrm{0}\left({equation}\:{dif}\right) \\ $$$$ \\ $$
Commented by Spillover last updated on 25/Feb/23
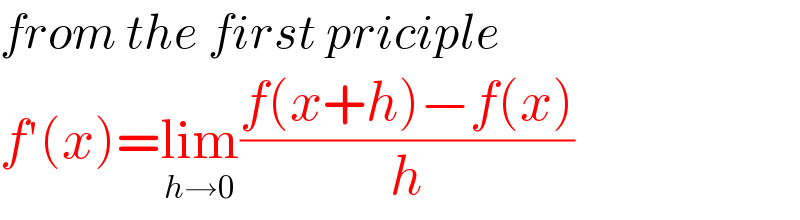
$${from}\:{the}\:{first}\:{priciple} \\ $$$${f}^{'} \left({x}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$
Answered by Mr_X last updated on 25/Feb/23
![Solution ⇒ y=xln(x) ⇒ y+Δy=(x+Δx)[ln(x+Δx)] ⇒ Δy=(x+Δx)[ln(x+Δx)]−xln(x) ⇒ Δy=(x+Δx){ln[(x)(1+((Δx)/x))]}−xln(x) ⇒ Δy=(x+Δx)[ln(x)+ln(1+((Δx)/x))]−xln(x) ⇒ Δy=xln(x)+Δxln(x)+xln(1+((Δx)/x))+Δxln(1+((Δx)/x))−xln(x) ⇒ ((Δy)/(Δx))=ln(x)+(x/(Δx))ln(1+((Δx)/x))+ln(1+((Δx)/x)) ⇒ ((Δy)/(Δx))=ln(x)+ln[(1+((Δx)/x))]^(x/(Δx)) +ln(1+((Δx)/x)) ⇒ lim_(Δx→0) ((Δy)/(Δx))=ln(x)+lim_(Δx→0) ln[(1+((Δx)/x))]^(x/(Δx)) +lim_(Δx→0) ln(1+((Δx)/x)) ⇒ (dy/dx)=ln(x)+ln[lim_(Δx→0) (1+((Δx)/x))]^(x/(Δx)) +lim_(Δx→0) ln(1+((Δx)/x)) ⇒ (dy/dx)=ln(x)+ln(e)+ln(1) ⇒ (dy/dx)=ln(x)+1+0 or ⇒ (dy/dx)=ln(x)+1](Q188070.png)
$${Solution}\:\Rightarrow \\ $$$${y}={xln}\left({x}\right) \\ $$$$\Rightarrow\:{y}+\Delta{y}=\left({x}+\Delta{x}\right)\left[{ln}\left({x}+\Delta{x}\right)\right] \\ $$$$\Rightarrow\:\Delta{y}=\left({x}+\Delta{x}\right)\left[{ln}\left({x}+\Delta{x}\right)\right]−{xln}\left({x}\right) \\ $$$$\Rightarrow\:\Delta{y}=\left({x}+\Delta{x}\right)\left\{{ln}\left[\left({x}\right)\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right)\right]\right\}−{xln}\left({x}\right) \\ $$$$\Rightarrow\:\Delta{y}=\left({x}+\Delta{x}\right)\left[{ln}\left({x}\right)+{ln}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right)\right]−{xln}\left({x}\right) \\ $$$$\Rightarrow\:\Delta{y}={xln}\left({x}\right)+\Delta{xln}\left({x}\right)+{xln}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right)+\Delta{xln}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right)−{xln}\left({x}\right) \\ $$$$\Rightarrow\:\frac{\Delta{y}}{\Delta{x}}={ln}\left({x}\right)+\frac{{x}}{\Delta{x}}{ln}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right)+{ln}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right) \\ $$$$\Rightarrow\:\frac{\Delta{y}}{\Delta{x}}={ln}\left({x}\right)+{ln}\left[\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right)\right]^{\frac{{x}}{\Delta{x}}} +{ln}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right) \\ $$$$\Rightarrow\:\underset{\Delta{x}\rightarrow\mathrm{0}} {{lim}}\frac{\Delta{y}}{\Delta{x}}={ln}\left({x}\right)+\underset{\Delta{x}\rightarrow\mathrm{0}} {{lim}ln}\left[\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right)\right]^{\frac{{x}}{\Delta{x}}} +\underset{\Delta{x}\rightarrow\mathrm{0}} {{lim}ln}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right) \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}={ln}\left({x}\right)+{ln}\left[\underset{\Delta{x}\rightarrow\mathrm{0}} {{lim}}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right)\right]^{\frac{{x}}{\Delta{x}}} +\underset{\Delta{x}\rightarrow\mathrm{0}} {{lim}ln}\left(\mathrm{1}+\frac{\Delta{x}}{{x}}\right) \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}={ln}\left({x}\right)+{ln}\left({e}\right)+{ln}\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}={ln}\left({x}\right)+\mathrm{1}+\mathrm{0} \\ $$$${or} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}={ln}\left({x}\right)+\mathrm{1} \\ $$
Commented by Michaelfaraday last updated on 01/Mar/23

$${thanks}\:{sir} \\ $$
