
Previous in Differential Equation Next in Differential Equation
Question Number 216787 by Engr_Jidda last updated on 20/Feb/25
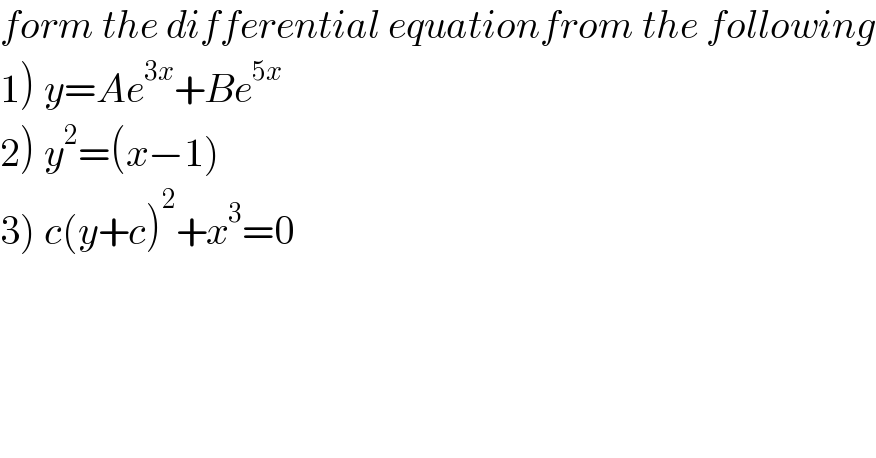
$${form}\:{the}\:{differential}\:{equationfrom}\:{the}\:{following} \\ $$$$\left.\mathrm{1}\right)\:{y}={Ae}^{\mathrm{3}{x}} +{Be}^{\mathrm{5}{x}} \\ $$$$\left.\mathrm{2}\right)\:{y}^{\mathrm{2}} =\left({x}−\mathrm{1}\right) \\ $$$$\left.\mathrm{3}\right)\:{c}\left({y}+{c}\right)^{\mathrm{2}} +{x}^{\mathrm{3}} =\mathrm{0} \\ $$
Answered by som(math1967) last updated on 20/Feb/25
![1. y=Ae^(3x) +Be^(5x) y_1 =3Ae^(3x) +5Be^(5x) y_2 =9Ae^(3x) +25Be^(5x) 5y_1 −y_2 =6Ae^(3x) ∴Ae^(3x) =((5y_1 −y_2 )/6) again y_2 −3y_1 =10Be^(5x) ∴ Be^(5x) =((y_2 −3y_1 )/(10)) ⇒ Ae^(3x) +Be^(5x) =((5y_1 −y_2 )/6) +((y_2 −3y_1 )/(10)) ⇒y=((25y_1 −5y_2 +3y_2 −9y_1 )/(30)) [y=Ae^(3x) +Be^(5x) ] ⇒y=((16y_1 −2y_2 )/(30)) ⇒y=((8y_1 −y_2 )/(15)) ∴ y_2 −8y_1 +15y=0](Q216791.png)
$$\:\mathrm{1}.\:{y}={Ae}^{\mathrm{3}{x}} +{Be}^{\mathrm{5}{x}} \\ $$$$\:{y}_{\mathrm{1}} =\mathrm{3}{Ae}^{\mathrm{3}{x}} +\mathrm{5}{Be}^{\mathrm{5}{x}} \\ $$$$\:{y}_{\mathrm{2}} =\mathrm{9}{Ae}^{\mathrm{3}{x}} +\mathrm{25}{Be}^{\mathrm{5}{x}} \\ $$$$\:\mathrm{5}{y}_{\mathrm{1}} −{y}_{\mathrm{2}} =\mathrm{6}{Ae}^{\mathrm{3}{x}} \\ $$$$\therefore{Ae}^{\mathrm{3}{x}} =\frac{\mathrm{5}{y}_{\mathrm{1}} −{y}_{\mathrm{2}} }{\mathrm{6}} \\ $$$${again}\:{y}_{\mathrm{2}} −\mathrm{3}{y}_{\mathrm{1}} =\mathrm{10}{Be}^{\mathrm{5}{x}} \\ $$$$\:\therefore\:{Be}^{\mathrm{5}{x}} =\frac{{y}_{\mathrm{2}} −\mathrm{3}{y}_{\mathrm{1}} }{\mathrm{10}} \\ $$$$\Rightarrow\:{Ae}^{\mathrm{3}{x}} +{Be}^{\mathrm{5}{x}} =\frac{\mathrm{5}{y}_{\mathrm{1}} −{y}_{\mathrm{2}} }{\mathrm{6}}\:+\frac{{y}_{\mathrm{2}} −\mathrm{3}{y}_{\mathrm{1}} }{\mathrm{10}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{25}{y}_{\mathrm{1}} −\mathrm{5}{y}_{\mathrm{2}} +\mathrm{3}{y}_{\mathrm{2}} −\mathrm{9}{y}_{\mathrm{1}} }{\mathrm{30}}\:\left[{y}={Ae}^{\mathrm{3}{x}} +{Be}^{\mathrm{5}{x}} \right] \\ $$$$\Rightarrow{y}=\frac{\mathrm{16}{y}_{\mathrm{1}} −\mathrm{2}{y}_{\mathrm{2}} }{\mathrm{30}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{8}{y}_{\mathrm{1}} −{y}_{\mathrm{2}} }{\mathrm{15}} \\ $$$$\:\therefore\:{y}_{\mathrm{2}} −\mathrm{8}{y}_{\mathrm{1}} +\mathrm{15}{y}=\mathrm{0} \\ $$
Commented by Engr_Jidda last updated on 20/Feb/25
$${wow}\:{thank}\:{you}\:{so}\:{much} \\ $$
