
Question Number 61210 by pooja24 last updated on 30/May/19
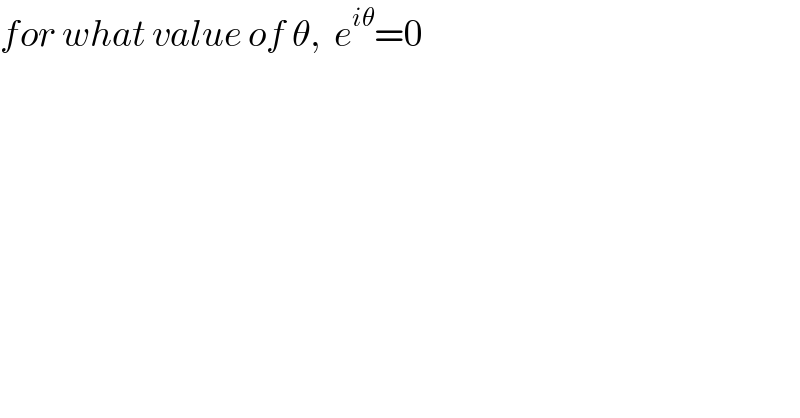
$${for}\:{what}\:{value}\:{of}\:\theta,\:\:{e}^{{i}\theta} =\mathrm{0}\:\: \\ $$
Commented by Tony Lin last updated on 30/May/19
![e^(iθ) =cosθ+isinθ cosθ∈[−1,1]∈R sinθ∈[−1,1]∈R ⇒if e^(iθ) =0, then sinθ must be 0 ⇒cosθ must be 0 but cos^2 θ+sin^2 θ=1 ⇒e^(iθ) ≠0](Q61212.png)
$${e}^{{i}\theta} ={cos}\theta+{isin}\theta \\ $$$$\:\:\:\:\:{cos}\theta\in\left[−\mathrm{1},\mathrm{1}\right]\in{R} \\ $$$$\:\:\:\:\:{sin}\theta\in\left[−\mathrm{1},\mathrm{1}\right]\in{R} \\ $$$$\Rightarrow{if}\:{e}^{{i}\theta} =\mathrm{0},\:{then}\:{sin}\theta\:{must}\:{be}\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{cos}\theta\:{must}\:{be}\:\mathrm{0} \\ $$$${but}\:{cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$$\Rightarrow{e}^{{i}\theta} \neq\mathrm{0} \\ $$
Answered by MJS last updated on 30/May/19
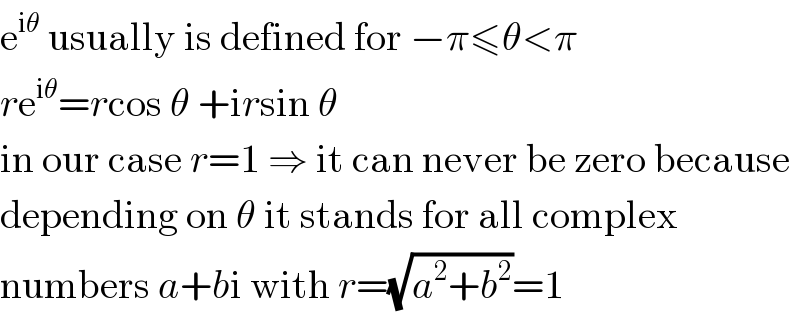
$$\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{usually}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:−\pi\leqslant\theta<\pi \\ $$$${r}\mathrm{e}^{\mathrm{i}\theta} ={r}\mathrm{cos}\:\theta\:+\mathrm{i}{r}\mathrm{sin}\:\theta \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case}\:{r}=\mathrm{1}\:\Rightarrow\:\mathrm{it}\:\mathrm{can}\:\mathrm{never}\:\mathrm{be}\:\mathrm{zero}\:\mathrm{because} \\ $$$$\mathrm{depending}\:\mathrm{on}\:\theta\:\mathrm{it}\:\mathrm{stands}\:\mathrm{for}\:\mathrm{all}\:\mathrm{complex} \\ $$$$\mathrm{numbers}\:{a}+{b}\mathrm{i}\:\mathrm{with}\:{r}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\mathrm{1} \\ $$
Answered by aleks041103 last updated on 31/May/19

$$\theta\rightarrow{i}\:\infty \\ $$$$\Rightarrow{e}^{{i}\theta} ={e}^{−\infty} =\mathrm{0} \\ $$
