Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 207096 by Wuji last updated on 06/May/24

for the given system of ODEs, calculate the eigenvalues and corresponding eigenvectors of the coefficient matrix (dx/dt)=2x+y (dy/dt)=x+2y

$${for}\:{the}\:{given}\:{system}\:{of}\:{ODEs},\:{calculate}\:{the} \\ $$$${eigenvalues}\:{and}\:{corresponding}\:{eigenvectors}\:{of}\:{the}\: \\ $$$${coefficient}\:{matrix} \\ $$$$\frac{{dx}}{{dt}}=\mathrm{2}{x}+{y}\:\:\:\frac{{dy}}{{dt}}={x}+\mathrm{2}{y} \\ $$

Commented by Wuji last updated on 07/May/24

need a helping hand, please

$${need}\:{a}\:{helping}\:{hand},\:{please} \\ $$

Commented by aleks041103 last updated on 07/May/24

the idea is if q= ((x),(y) ) and also then (dq/dt)= (((dx/dt)),((dy/dt)) ) then you can write the linear ODE as (dq/dt)=M^� q where M^� is the coefficient matrix ⇒ in this case the coeff matrix is ((2,1),(1,2) )... try from here yourself

$${the}\:{idea}\:{is}\: \\ $$$${if}\:\:\:\boldsymbol{{q}}=\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:{and}\:{also}\:{then}\:\:\frac{{d}\boldsymbol{{q}}}{{dt}}=\begin{pmatrix}{{dx}/{dt}}\\{{dy}/{dt}}\end{pmatrix} \\ $$$${then}\:{you}\:{can}\:{write}\:{the}\:{linear}\:{ODE}\:{as} \\ $$$$\frac{{d}\boldsymbol{{q}}}{{dt}}=\hat {{M}}\:\boldsymbol{{q}}\: \\ $$$${where}\:\hat {{M}}\:{is}\:{the}\:{coefficient}\:{matrix} \\ $$$$ \\ $$$$\Rightarrow\:{in}\:{this}\:{case}\:{the}\:{coeff}\:{matrix}\:{is} \\ $$$$\begin{pmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{1}}&{\mathrm{2}}\end{pmatrix}... \\ $$$${try}\:{from}\:{here}\:{yourself} \\ $$

Commented by Wuji last updated on 07/May/24

yes, sir. thank you so much

$$\mathrm{yes},\:\mathrm{sir}.\:\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Answered by mr W last updated on 07/May/24

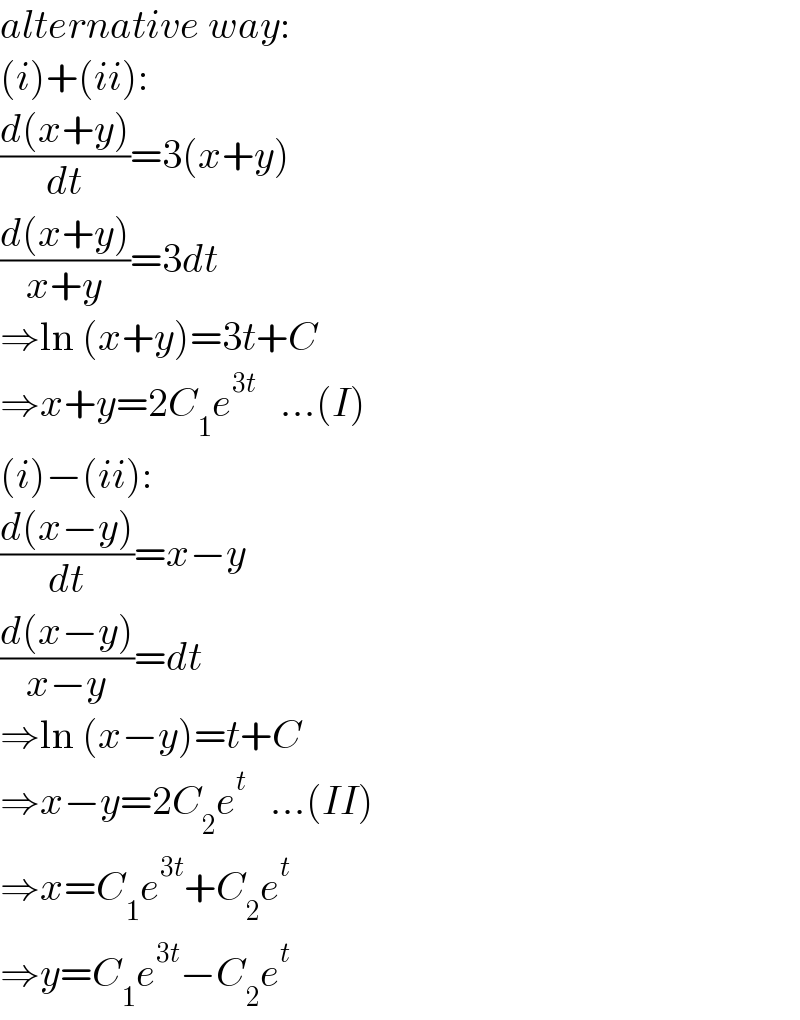
alternative way: (i)+(ii): ((d(x+y))/dt)=3(x+y) ((d(x+y))/(x+y))=3dt ⇒ln (x+y)=3t+C ⇒x+y=2C_1 e^(3t) ...(I) (i)−(ii): ((d(x−y))/dt)=x−y ((d(x−y))/(x−y))=dt ⇒ln (x−y)=t+C ⇒x−y=2C_2 e^t ...(II) ⇒x=C_1 e^(3t) +C_2 e^t ⇒y=C_1 e^(3t) −C_2 e^t

$${alternative}\:{way}: \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\frac{{d}\left({x}+{y}\right)}{{dt}}=\mathrm{3}\left({x}+{y}\right) \\ $$$$\frac{{d}\left({x}+{y}\right)}{{x}+{y}}=\mathrm{3}{dt} \\ $$$$\Rightarrow\mathrm{ln}\:\left({x}+{y}\right)=\mathrm{3}{t}+{C} \\ $$$$\Rightarrow{x}+{y}=\mathrm{2}{C}_{\mathrm{1}} {e}^{\mathrm{3}{t}} \:\:\:...\left({I}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\frac{{d}\left({x}−{y}\right)}{{dt}}={x}−{y} \\ $$$$\frac{{d}\left({x}−{y}\right)}{{x}−{y}}={dt} \\ $$$$\Rightarrow\mathrm{ln}\:\left({x}−{y}\right)={t}+{C} \\ $$$$\Rightarrow{x}−{y}=\mathrm{2}{C}_{\mathrm{2}} {e}^{{t}} \:\:\:...\left({II}\right) \\ $$$$\Rightarrow{x}={C}_{\mathrm{1}} {e}^{\mathrm{3}{t}} +{C}_{\mathrm{2}} {e}^{{t}} \\ $$$$\Rightarrow{y}={C}_{\mathrm{1}} {e}^{\mathrm{3}{t}} −{C}_{\mathrm{2}} {e}^{{t}} \\ $$

Commented by Wuji last updated on 07/May/24

God bless you, sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you},\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com