
Question Number 53262 by Tawa1 last updated on 19/Jan/19
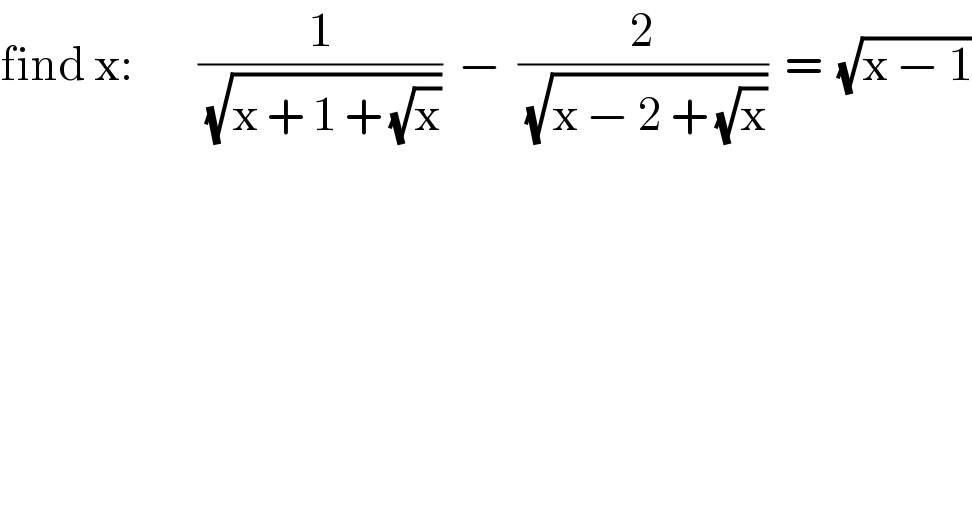
$$\mathrm{find}\:\mathrm{x}:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{x}\:+\:\mathrm{1}\:+\:\sqrt{\mathrm{x}}}}\:\:−\:\:\frac{\mathrm{2}}{\sqrt{\mathrm{x}\:−\:\mathrm{2}\:+\:\sqrt{\mathrm{x}}}}\:\:=\:\:\sqrt{\mathrm{x}\:−\:\mathrm{1}} \\ $$
Commented by mr W last updated on 20/Jan/19

$${there}\:{is}\:{no}\:{real}\:{solution}! \\ $$$${LHS}: \\ $$$${say}\:{x}+\sqrt{{x}}={u}\:>\mathrm{2} \\ $$$$\sqrt{{u}+\mathrm{1}}>\sqrt{{u}−\mathrm{2}}\:>\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\sqrt{{u}+\mathrm{1}}}<\frac{\mathrm{1}}{\sqrt{{u}−\mathrm{2}}}<\frac{\mathrm{2}}{\sqrt{{u}−\mathrm{2}}} \\ $$$$\Rightarrow{LHS}=\frac{\mathrm{1}}{\sqrt{{x}+\mathrm{1}+\sqrt{{x}}}}−\frac{\mathrm{2}}{\sqrt{{x}−\mathrm{2}+\sqrt{{x}}}}=\frac{\mathrm{1}}{\sqrt{{u}+\mathrm{1}}}−\frac{\mathrm{2}}{\sqrt{{u}−\mathrm{2}}}<\mathrm{0} \\ $$$$ \\ $$$${RHS}: \\ $$$$\sqrt{{x}−\mathrm{1}}\geqslant\mathrm{0} \\ $$$$ \\ $$$${i}.{e}.\:{LHS}\:{is}\:{always}\:{negative},\:{but}\:{RHS} \\ $$$${is}\:{always}\:{positive}\:{or}\:{zero}. \\ $$$${LHS}<\mathrm{0}\:\neq\:{RHS}\geqslant\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{no}\:{solution}\:{for}\:{LHS}={RHS}! \\ $$
Commented by Tawa1 last updated on 20/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Jan/19

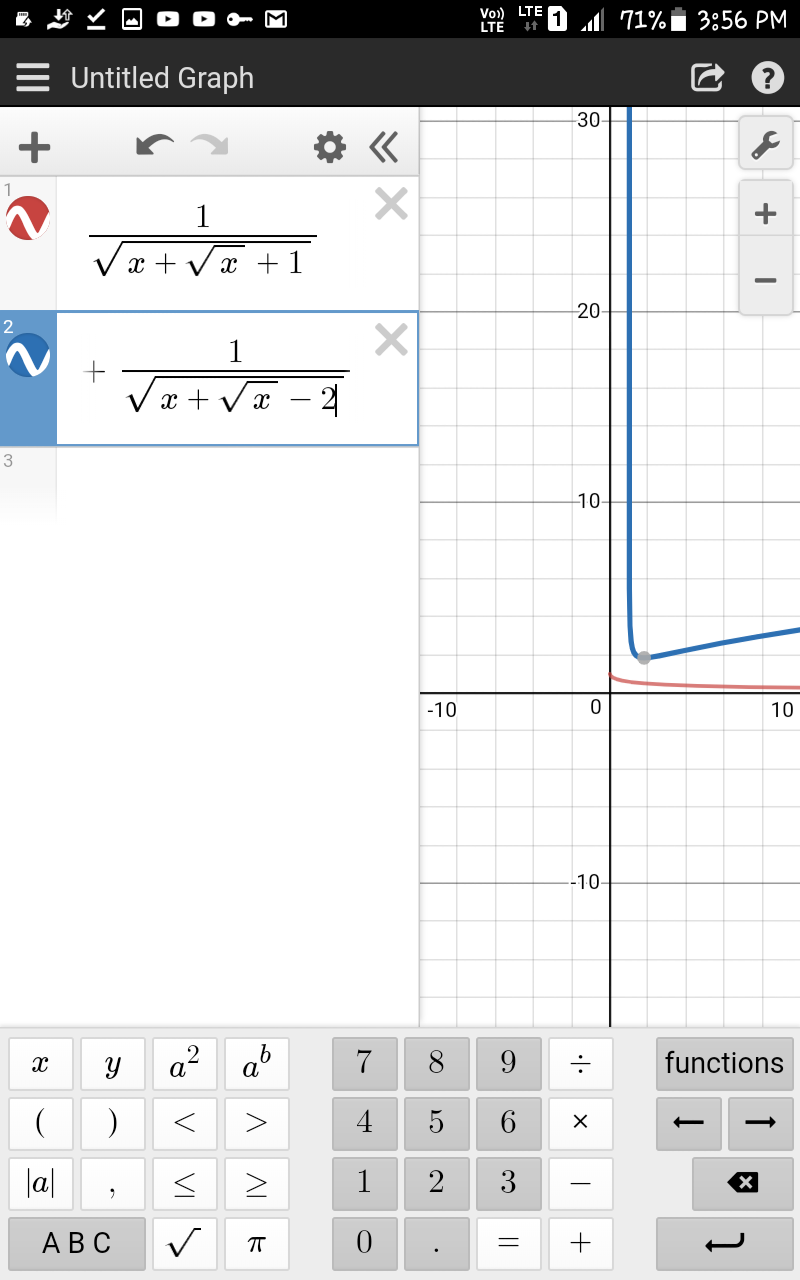
$${condition}... \\ $$$$\left.\mathrm{1}\right){x}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\left({x}−\mathrm{1}\right)>\mathrm{0}\:{i},{e}\:{x}>\mathrm{1} \\ $$$$\left.\mathrm{3}\right){x}−\mathrm{2}+\sqrt{{x}}\:>\mathrm{0} \\ $$$${if}\:{x}=\mathrm{1}\:\:{then}\:{x}−\mathrm{2}+\sqrt{{x}}\:=\mathrm{0} \\ $$$${but}\:{value}\:{of}\:{x}+\sqrt{{x}\:}\:{should}\:{be}\:{greater}\:{than}\:\mathrm{2} \\ $$$${so}\:{x}\:{should}\:{be}\:{x}>\mathrm{1} \\ $$$$\left.\mathrm{4}\right){x}+\mathrm{1}+\sqrt{{x}}\:>\mathrm{0}\:{when}\:{x}>\mathrm{1} \\ $$$${so}\:{x}\:{should}\:{be}\:{greater}\:{than}\:\mathrm{1} \\ $$$${wait}... \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\sqrt{{x}+\sqrt{{x}}++\mathrm{1}}} \\ $$$${g}\left({x}\right)=\sqrt{{x}−\mathrm{1}}\:+\frac{\mathrm{1}}{\sqrt{{x}+\sqrt{{x}}\:−\mathrm{2}}} \\ $$$${from}\:{graph}\:{it}\:{is}\:{confirmed}\:{that}\:{f}\left({x}\right)\:{never} \\ $$$${intersect}\:{g}\left({x}\right)\:\:\:{hence}\:\:{no}\:{solution}... \\ $$$${however}... \\ $$$${condition}\:{of}\:{two}\:{curve}\:{intesect}/{touch}\:{is}\:{shortest} \\ $$$${distance}\:{zero}.. \\ $$$$ \\ $$
Commented by Tawa1 last updated on 20/Jan/19
$$\mathrm{Alright}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{wait}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Jan/19

