
Question Number 207747 by MASANJAJJ last updated on 25/May/24
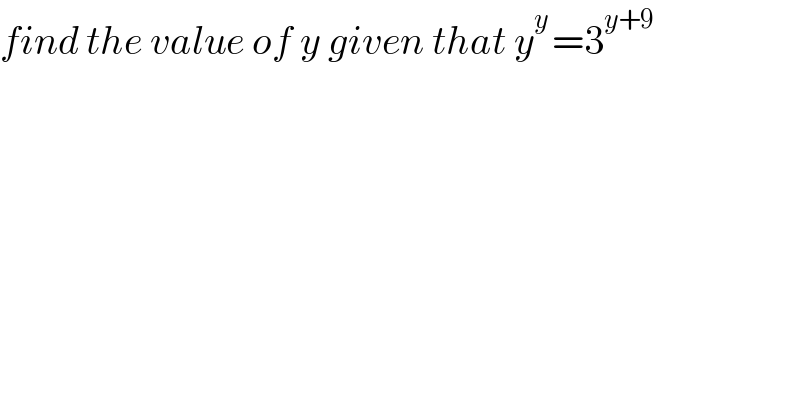
$${find}\:{the}\:{value}\:{of}\:{y}\:{given}\:{that}\:{y}^{{y}\:} =\mathrm{3}^{{y}+\mathrm{9}} \\ $$
Answered by mr W last updated on 25/May/24
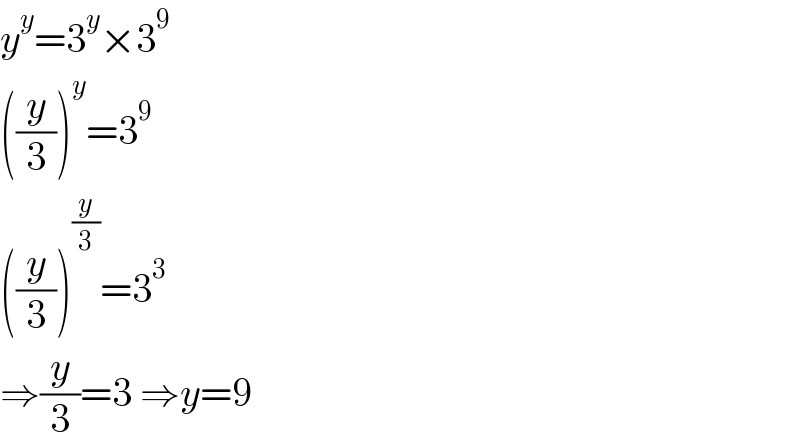
$${y}^{{y}} =\mathrm{3}^{{y}} ×\mathrm{3}^{\mathrm{9}} \\ $$$$\left(\frac{{y}}{\mathrm{3}}\right)^{{y}} =\mathrm{3}^{\mathrm{9}} \\ $$$$\left(\frac{{y}}{\mathrm{3}}\right)^{\frac{{y}}{\mathrm{3}}} =\mathrm{3}^{\mathrm{3}} \\ $$$$\Rightarrow\frac{{y}}{\mathrm{3}}=\mathrm{3}\:\Rightarrow{y}=\mathrm{9} \\ $$
Answered by Berbere last updated on 25/May/24
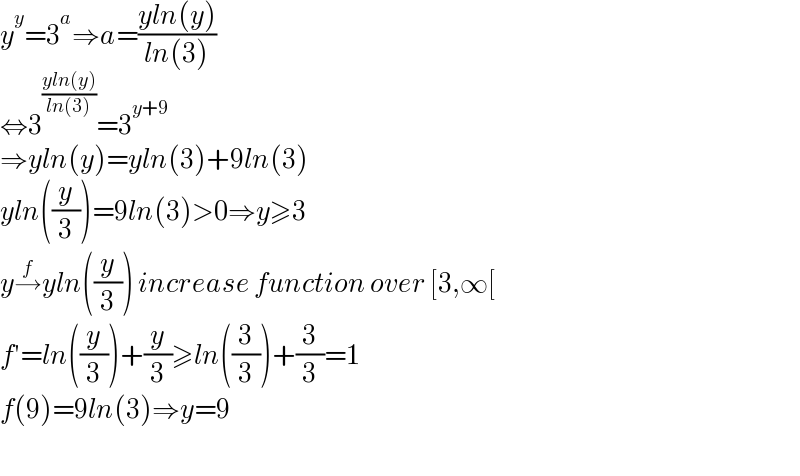
$${y}^{{y}} =\mathrm{3}^{{a}} \Rightarrow{a}=\frac{{yln}\left({y}\right)}{{ln}\left(\mathrm{3}\right)} \\ $$$$\Leftrightarrow\mathrm{3}^{\frac{{yln}\left({y}\right)}{{ln}\left(\mathrm{3}\right)}} =\mathrm{3}^{{y}+\mathrm{9}} \\ $$$$\Rightarrow{yln}\left({y}\right)={yln}\left(\mathrm{3}\right)+\mathrm{9}{ln}\left(\mathrm{3}\right) \\ $$$${yln}\left(\frac{{y}}{\mathrm{3}}\right)=\mathrm{9}{ln}\left(\mathrm{3}\right)>\mathrm{0}\Rightarrow{y}\geqslant\mathrm{3} \\ $$$${y}\overset{{f}} {\rightarrow}{yln}\left(\frac{{y}}{\mathrm{3}}\right)\:{increase}\:{function}\:{over}\:\left[\mathrm{3},\infty\left[\right.\right. \\ $$$${f}'={ln}\left(\frac{{y}}{\mathrm{3}}\right)+\frac{{y}}{\mathrm{3}}\geqslant{ln}\left(\frac{\mathrm{3}}{\mathrm{3}}\right)+\frac{\mathrm{3}}{\mathrm{3}}=\mathrm{1} \\ $$$${f}\left(\mathrm{9}\right)=\mathrm{9}{ln}\left(\mathrm{3}\right)\Rightarrow{y}=\mathrm{9} \\ $$$$ \\ $$
Answered by Berbere last updated on 25/May/24
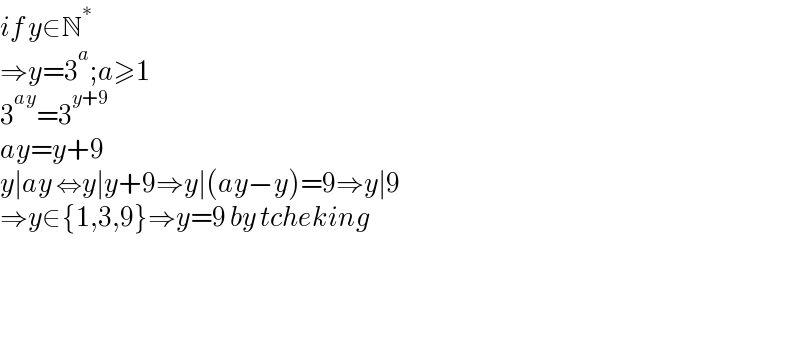
$${if}\:{y}\in\mathbb{N}^{\ast} \\ $$$$\Rightarrow{y}=\mathrm{3}^{{a}} ;{a}\geqslant\mathrm{1} \\ $$$$\mathrm{3}^{{ay}} =\mathrm{3}^{{y}+\mathrm{9}} \\ $$$${ay}={y}+\mathrm{9} \\ $$$${y}\mid{ay}\:\Leftrightarrow{y}\mid{y}+\mathrm{9}\Rightarrow{y}\mid\left({ay}−{y}\right)=\mathrm{9}\Rightarrow{y}\mid\mathrm{9} \\ $$$$\Rightarrow{y}\in\left\{\mathrm{1},\mathrm{3},\mathrm{9}\right\}\Rightarrow{y}=\mathrm{9}\:{by}\:{tcheking} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
