Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 191528 by mnjuly1970 last updated on 25/Apr/23

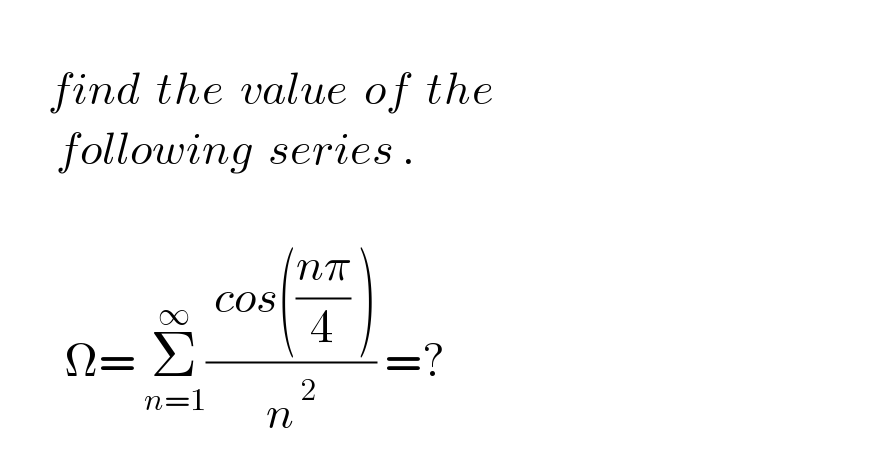
find the value of the following series . Ω= Σ_(n=1) ^∞ (( cos(((nπ)/4) ))/n^( 2) ) =?

$$ \\ $$$$\:\:\:\:\:\:{find}\:\:{the}\:\:{value}\:\:{of}\:\:{the} \\ $$$$\:\:\:\:\:\:\:{following}\:\:{series}\:. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\Omega=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:{cos}\left(\frac{{n}\pi}{\mathrm{4}}\:\right)}{{n}^{\:\mathrm{2}} }\:=? \\ $$

Answered by witcher3 last updated on 25/Apr/23

Σ_(n≥1) ((cos(n(π/4)))/n^2 )=(1/2)Σ_(n≥1) (((e^((iπ)/4) )^n +(e^(−((iπ)/4)) )^n )/n^2 ) =(1/2){Σ_(n≥1) (((e^((iπ)/4) )^n )/n^2 )+Σ_(n≥1) (((e^(−((iπ)/4)) )^n )/n^2 )} =(1/2)(Li_2 (e^(i(π/4)) )+Li_2 (e^(−((iπ)/4)) )) Li_2 (z)+Li_2 ((1/z))=−ζ(2)−(1/2)ln^2 (−z) Ω=(1/2)(Li_2 (e^(−((iπ)/4)) )+Li_2 ((1/e^(−((iπ)/4)) ))) =(1/2)(−(𝛑^2 /6)−(1/2)ln^2 (−e^(−((iπ)/4)) ))=(1/2)(−(π^2 /6)+((9π^2 )/(32))) =((11π^2 )/(192))

$$\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{cos}\left(\mathrm{n}\frac{\pi}{\mathrm{4}}\right)}{\mathrm{n}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{n}} +\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }+\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{Li}_{\mathrm{2}} \left(\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)+\mathrm{Li}_{\mathrm{2}} \left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\right) \\ $$$$\mathrm{Li}_{\mathrm{2}} \left(\mathrm{z}\right)+\mathrm{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{z}}\right)=−\zeta\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(−\mathrm{z}\right) \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{Li}_{\mathrm{2}} \left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)+\mathrm{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} }\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{9}\pi^{\mathrm{2}} }{\mathrm{32}}\right) \\ $$$$=\frac{\mathrm{11}\pi^{\mathrm{2}} }{\mathrm{192}} \\ $$

Commented by mnjuly1970 last updated on 25/Apr/23

thanks alot ....sir

$${thanks}\:{alot}\:....{sir} \\ $$

Commented by witcher3 last updated on 25/Apr/23

withe Pleasur Sir

$$\mathrm{withe}\:\mathrm{Pleasur}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com