
Question Number 57817 by Abdo msup. last updated on 12/Apr/19
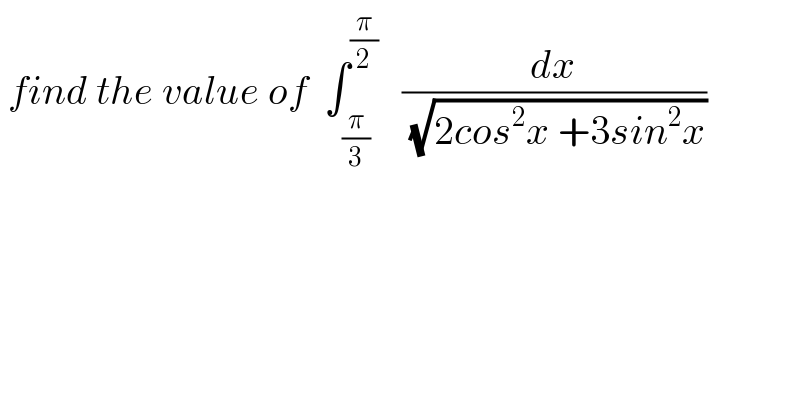
$$\:{find}\:{the}\:{value}\:{of}\:\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dx}}{\sqrt{\mathrm{2}{cos}^{\mathrm{2}} {x}\:+\mathrm{3}{sin}^{\mathrm{2}} {x}}} \\ $$
Commented by mr W last updated on 13/Apr/19
Incomplete elliptic integral of the first kind, no elementary solution.
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19
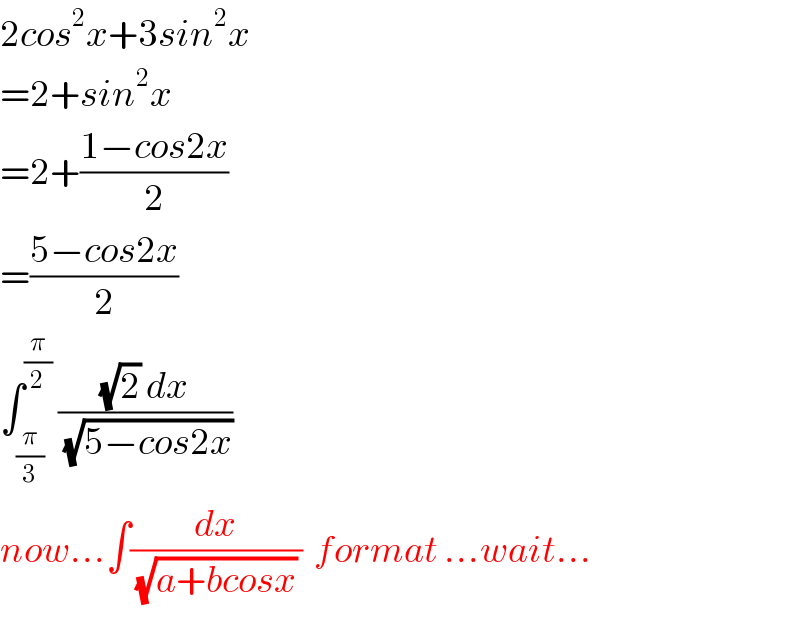
$$\mathrm{2}{cos}^{\mathrm{2}} {x}+\mathrm{3}{sin}^{\mathrm{2}} {x} \\ $$$$=\mathrm{2}+{sin}^{\mathrm{2}} {x} \\ $$$$=\mathrm{2}+\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{5}−{cos}\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\sqrt{\mathrm{2}}\:{dx}}{\sqrt{\mathrm{5}−{cos}\mathrm{2}{x}}} \\ $$$${now}...\int\frac{{dx}}{\sqrt{{a}+{bcosx}}\:}\:\:{format}\:...{wait}... \\ $$
