
Question Number 34862 by a.i msup by abdo last updated on 12/May/18
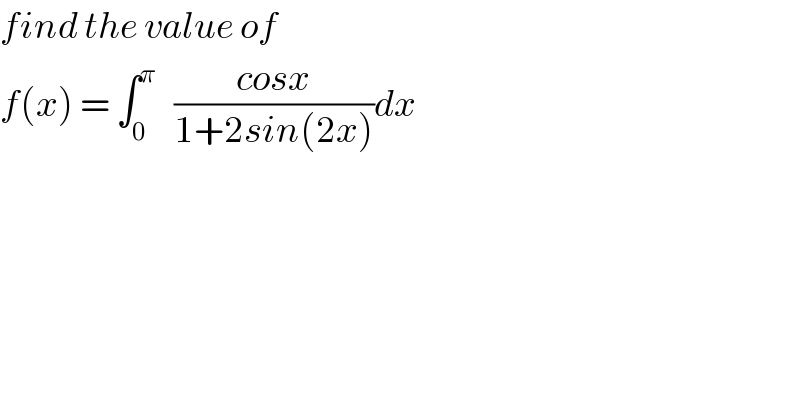
$${find}\:{the}\:{value}\:{of} \\ $$$${f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{cosx}}{\mathrm{1}+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$
Commented by prof Abdo imad last updated on 14/May/18

$${thank}\:{you}\:{sir}\:{for}\:{this}\:{remark}..{i}\:{have}\:{working} \\ $$$${a}\:{lot}\:{in}\:{complexe}\:{analysis}\:{but}\:{i}\:{find}\:{often} \\ $$$${something}\:{that}\:{we}\:{can}\:{t}\:\:{understand}\:{and} \\ $$$${explain}\:\:{it}\:{s}\:{more}\:{and}\:{more}\:{difficult}... \\ $$
Commented by prof Abdo imad last updated on 12/May/18
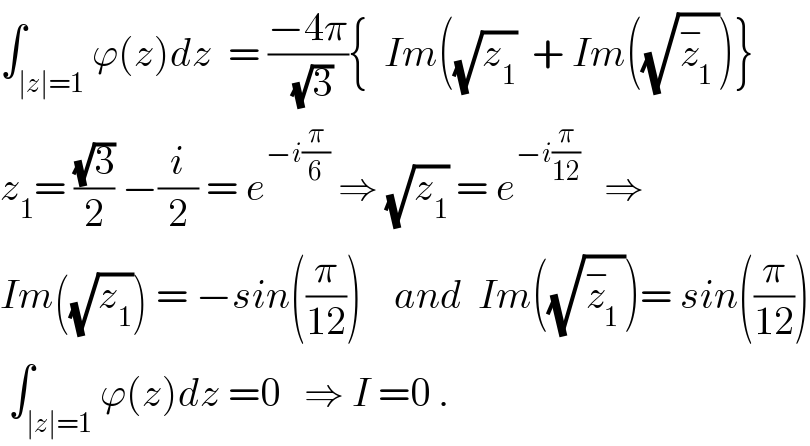
$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:\:=\:\frac{−\mathrm{4}\pi}{\sqrt{\mathrm{3}}}\left\{\:\:{Im}\left(\sqrt{{z}_{\mathrm{1}} }\:\:+\:{Im}\left(\sqrt{\overset{−} {{z}}_{\mathrm{1}} }\right)\right\}\right. \\ $$$${z}_{\mathrm{1}} =\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:−\frac{{i}}{\mathrm{2}}\:=\:{e}^{−{i}\frac{\pi}{\mathrm{6}}} \:\Rightarrow\:\sqrt{{z}_{\mathrm{1}} }\:=\:{e}^{−{i}\frac{\pi}{\mathrm{12}}} \:\:\:\Rightarrow \\ $$$${Im}\left(\sqrt{{z}_{\mathrm{1}} }\right)\:=\:−{sin}\left(\frac{\pi}{\mathrm{12}}\right)\:\:\:\:{and}\:\:{Im}\left(\sqrt{\overset{−} {{z}}_{\mathrm{1}} }\right)=\:{sin}\left(\frac{\pi}{\mathrm{12}}\right) \\ $$$$\:\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{0}\:\:\:\Rightarrow\:{I}\:=\mathrm{0}\:. \\ $$
Commented by MJS last updated on 13/May/18
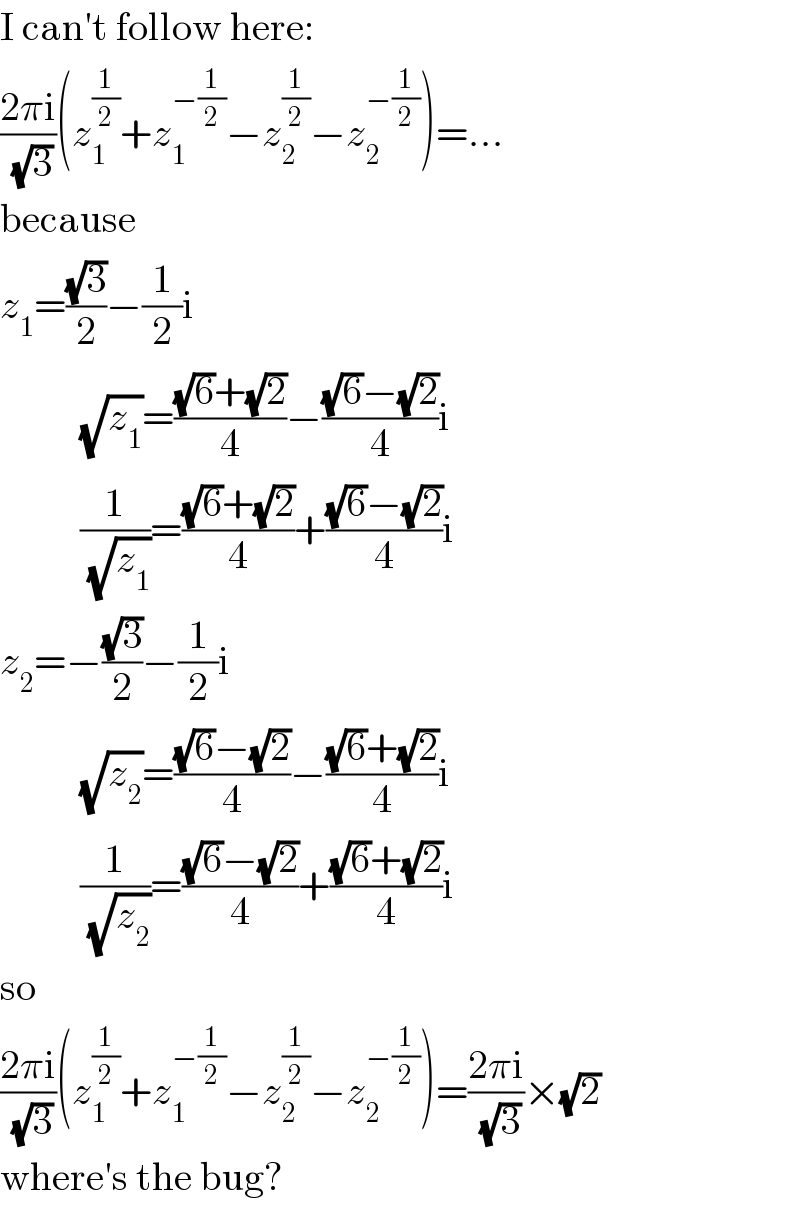
$$\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{follow}\:\mathrm{here}: \\ $$$$\frac{\mathrm{2}\pi\mathrm{i}}{\sqrt{\mathrm{3}}}\left({z}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} +{z}_{\mathrm{1}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} −{z}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{2}}} −{z}_{\mathrm{2}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)=... \\ $$$$\mathrm{because} \\ $$$${z}_{\mathrm{1}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\sqrt{{z}_{\mathrm{1}} }=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}−\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\sqrt{{z}_{\mathrm{1}} }}=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{i} \\ $$$${z}_{\mathrm{2}} =−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\sqrt{{z}_{\mathrm{2}} }=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}−\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\sqrt{{z}_{\mathrm{2}} }}=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{i} \\ $$$$\mathrm{so} \\ $$$$\frac{\mathrm{2}\pi\mathrm{i}}{\sqrt{\mathrm{3}}}\left({z}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} +{z}_{\mathrm{1}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} −{z}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{2}}} −{z}_{\mathrm{2}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)=\frac{\mathrm{2}\pi\mathrm{i}}{\sqrt{\mathrm{3}}}×\sqrt{\mathrm{2}} \\ $$$$\mathrm{where}'\mathrm{s}\:\mathrm{the}\:\mathrm{bug}? \\ $$
Commented by abdo mathsup 649 cc last updated on 13/May/18
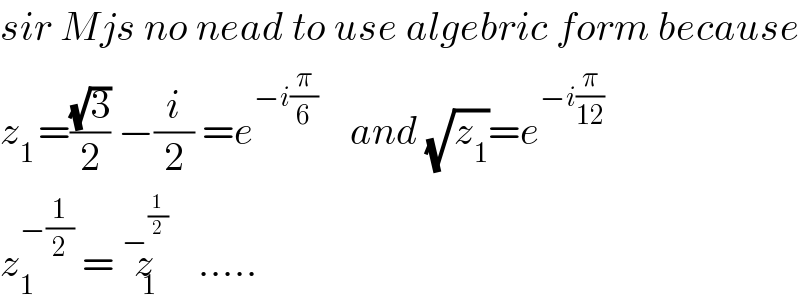
$${sir}\:{Mjs}\:{no}\:{nead}\:{to}\:{use}\:{algebric}\:{form}\:{because} \\ $$$${z}_{\mathrm{1}\:} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:−\frac{{i}}{\mathrm{2}}\:={e}^{−{i}\frac{\pi}{\mathrm{6}}} \:\:\:\:{and}\:\sqrt{{z}_{\mathrm{1}} }={e}^{−{i}\frac{\pi}{\mathrm{12}}} \\ $$$${z}_{\mathrm{1}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\overset{−^{\frac{\mathrm{1}}{\mathrm{2}}} } {{z}}_{\mathrm{1}} \:\:..... \\ $$
Commented by MJS last updated on 14/May/18
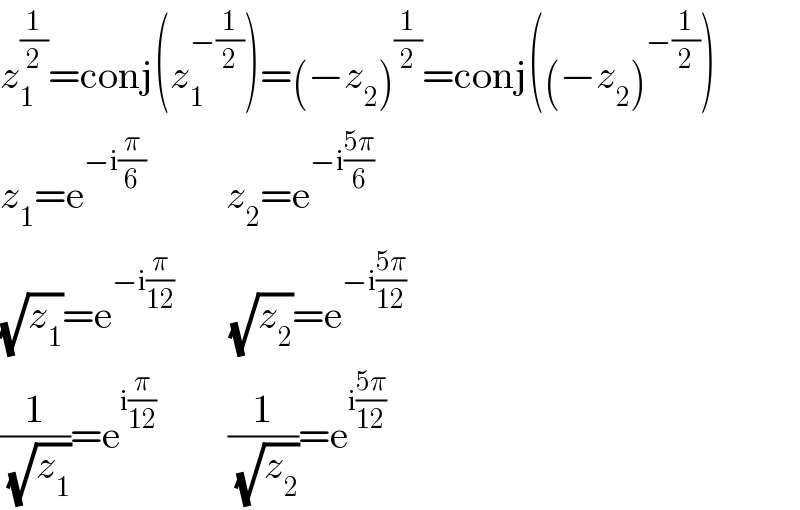
$${z}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{conj}\left({z}_{\mathrm{1}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)=\left(−{z}_{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{conj}\left(\left(−{z}_{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$$${z}_{\mathrm{1}} =\mathrm{e}^{−\mathrm{i}\frac{\pi}{\mathrm{6}}} \:\:\:\:\:\:\:\:\:\:{z}_{\mathrm{2}} =\mathrm{e}^{−\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{6}}} \\ $$$$\sqrt{{z}_{\mathrm{1}} }=\mathrm{e}^{−\mathrm{i}\frac{\pi}{\mathrm{12}}} \:\:\:\:\:\:\:\sqrt{{z}_{\mathrm{2}} }=\mathrm{e}^{−\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{12}}} \\ $$$$\frac{\mathrm{1}}{\sqrt{{z}_{\mathrm{1}} }}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{12}}} \:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\sqrt{{z}_{\mathrm{2}} }}=\mathrm{e}^{\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{12}}} \\ $$
Commented by MJS last updated on 14/May/18
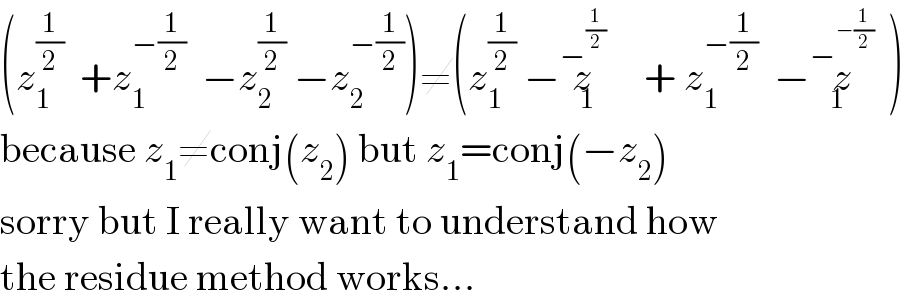
$$\left({z}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:+{z}_{\mathrm{1}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:−{z}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:−{z}_{\mathrm{2}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)\neq\left({z}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:−\overset{−^{\frac{\mathrm{1}}{\mathrm{2}}} } {{z}}_{\mathrm{1}} \:\:\:+\:{z}_{\mathrm{1}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:−\overset{−^{−\frac{\mathrm{1}}{\mathrm{2}}} } {{z}}_{\mathrm{1}} \right) \\ $$$$\mathrm{because}\:{z}_{\mathrm{1}} \neq\mathrm{conj}\left({z}_{\mathrm{2}} \right)\:\mathrm{but}\:{z}_{\mathrm{1}} =\mathrm{conj}\left(−{z}_{\mathrm{2}} \right) \\ $$$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{I}\:\mathrm{really}\:\mathrm{want}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{how} \\ $$$$\mathrm{the}\:\mathrm{residue}\:\mathrm{method}\:\mathrm{works}... \\ $$
Commented by abdo mathsup 649 cc last updated on 14/May/18

$${sir}\:{Mjs}\:{i}\:{will}\:{delet}\:{my}\:{method}\:{used}\:{in}\:{this}\:{integral} \\ $$$${and}\:{try}\:{another}\:{because}\:{the}\:{consept}\:{of}\:{residus} \\ $$$${is}\:{more}\:{difficult}\:{in}\:{some}\:{cases}.... \\ $$
Commented by MJS last updated on 14/May/18

$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{say}\:\mathrm{if}\:\mathrm{your}\:\mathrm{method}\:\mathrm{is}\:\mathrm{right}\:\mathrm{or} \\ $$$$\mathrm{wrong},\:\mathrm{I}'\mathrm{m}\:\mathrm{just}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{follow}\:\mathrm{and} \\ $$$$\mathrm{hopefully}\:\mathrm{understand}\:\mathrm{what}\:\mathrm{you}'\mathrm{re}\:\mathrm{doing}. \\ $$$$\mathrm{I}\:\mathrm{believe}\:\mathrm{you}'\mathrm{re}\:\mathrm{very}\:\mathrm{much}\:\mathrm{better}\:\mathrm{in}\:\mathrm{these} \\ $$$$\mathrm{things}\:\mathrm{than}\:\mathrm{I}\:\mathrm{am},\:\mathrm{since}\:\mathrm{I}\:\mathrm{had}\:\mathrm{been}\:\mathrm{studying} \\ $$$$\mathrm{maths}\:\mathrm{about}\:\mathrm{25}\:\mathrm{years}\:\mathrm{ago}\:\mathrm{and}\:\mathrm{I}\:\mathrm{have}\:\mathrm{forgotten} \\ $$$$\mathrm{many}\:\mathrm{things}...\:\mathrm{I}'\mathrm{ll}\:\mathrm{be}\:\mathrm{truly}\:\mathrm{thankful}\:\mathrm{for}\:\mathrm{any} \\ $$$$\mathrm{explanation}\:\mathrm{you}\:\mathrm{give}\:\mathrm{in}\:\mathrm{this}\:\mathrm{or}\:\mathrm{another}\:\mathrm{case} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/May/18

$${let}\:{k}={tanx}\:\:\:{dk}={sec}^{\mathrm{2}} {xdx} \\ $$$${I}'=\int\frac{{cosx}}{\mathrm{1}+\mathrm{4}{sinxcosx}} \\ $$$$=\int\frac{{cosx}}{\mathrm{1}+\mathrm{4}{tanx}.{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$=\int\frac{{cosx}}{{cos}^{\mathrm{2}} {x}\left({sec}^{\mathrm{2}} {x}+\mathrm{4}{tanx}\right)}{dx} \\ $$$$=\int\frac{{sec}^{\mathrm{2}} {x}\:{dx}}{{secx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}+\mathrm{4}{tanx}\right)} \\ $$$$=\int\frac{{dk}}{\left(\sqrt{\left.\mathrm{1}+{k}^{\mathrm{2}} \right)}\left(\mathrm{1}+{k}^{\mathrm{2}} +\mathrm{4}{k}\right)\right.} \\ $$$${contd} \\ $$
Answered by math1967 last updated on 12/May/18
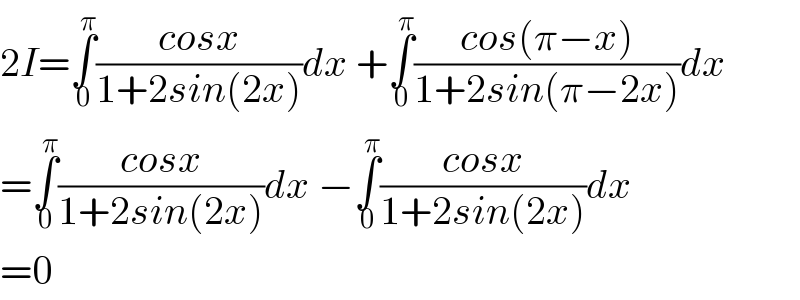
$$\mathrm{2}{I}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{cosx}}{\mathrm{1}+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)}{dx}\:+\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{cos}\left(\pi−{x}\right)}{\mathrm{1}+\mathrm{2}{sin}\left(\pi−\mathrm{2}{x}\right)}{dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{cosx}}{\mathrm{1}+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)}{dx}\:−\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{cosx}}{\mathrm{1}+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$$$=\mathrm{0} \\ $$
