Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 66065 by mathmax by abdo last updated on 08/Aug/19

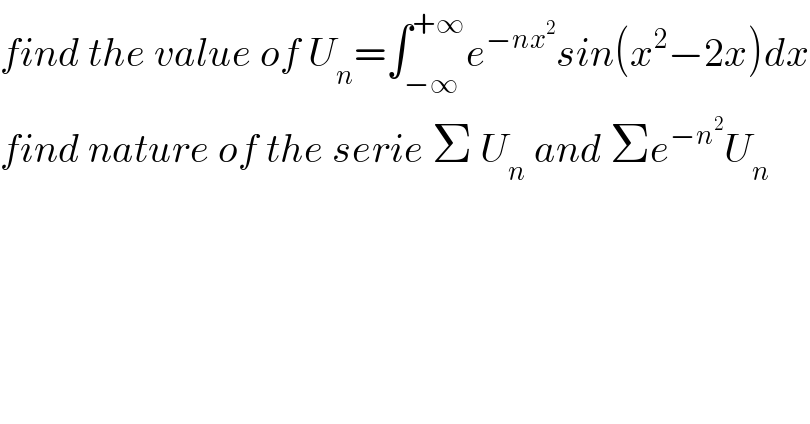
find the value of U_n =∫_(−∞) ^(+∞) e^(−nx^2 ) sin(x^2 −2x)dx find nature of the serie Σ U_n and Σe^(−n^2 ) U_n

$${find}\:{the}\:{value}\:{of}\:{U}_{{n}} =\int_{−\infty} ^{+\infty} {e}^{−{nx}^{\mathrm{2}} } {sin}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\right){dx} \\ $$$${find}\:{nature}\:{of}\:{the}\:{serie}\:\Sigma\:{U}_{{n}} \:{and}\:\Sigma{e}^{−{n}^{\mathrm{2}} } {U}_{{n}} \\ $$

Commented by mathmax by abdo last updated on 09/Aug/19

we have x^2 −2x =x^2 −2x +1−1 =(x−1)^2 −1 changement x−1 =t give U_n =∫_(−∞) ^(+∞) e^(−n(t+1)^2 ) sin(t^2 −1)dt =Im (∫_(−∞) ^(+∞) e^(−n(t+1)^2 +i(t^2 −1)) dt) =Im(W_n ) ∫_(−∞) ^(+∞) e^(−n(t+1)^2 +i(t^2 −1)) dt =∫_(−∞) ^(+∞) e^(−n(t^2 +2t+1)+it^2 −i) dt =e^(−i) ∫_(−∞) ^(+∞) e^(−(n−i)t^2 −2nt −n) dt =e^(−(n+i)) ∫_(−∞) ^(+∞) e^(−{((√(n−i))t)^2 +2nt}) dt =e^(−(n+i)) ∫_(−∞) ^(+∞) e^(−{ ((√(n−i))t)^2 +2(n/(√(n−i)))(√(n−i))t +((n/(√(n−i))))^2 −(n^2 /(n−i))}) dt =e^(−(n+i)) ∫_(−∞) ^(+∞) e^(−{(√(n−i))t +(n/(√(n−i)))}^2 +(n^2 /(n−i))) dt (ch. (√(n−i))t +(n/(√(n−i))) =v =e^((n^2 /(n−i))−(n+i)) ∫_(−∞) ^(+∞) e^(−v^2 ) (dv/(√(n−i))) =(√π)(1/(√(n−i))) e^((n^2 −(n^2 −i^2 ))/(n−i)) =((√π)/(√(n−i))) e^(−(1/(n−i))) =((√π)/(√(n−i))) e^(−((n+i)/(n^2 +1))) n−i =(√(1+n^2 )) e^(i arctan(((−1)/n))) =(√(1+n^2 ))e^(−iarctan((1/n))) ⇒ (√(n−i)) =(1+n^2 )^(1/4) e^(−(i/2)arctan((1/n))) ⇒ W_n =(√π)(1+n^2 )^(−(1/4)) e^((i/2)arctan((1/n))) e^(−(n/(n^2 +1))) e^(−(i/(n^2 +1))) =(√π)(n^2 +1)^(−(1/4)) e^(−(n/(n^2 +1))) e^(i((1/2)arctan((1/n))−(1/(n^2 +1)))) ⇒ U_n =(√π)(n^2 +1)^(−(1/4)) e^(−(n/(n^2 +1))) sin((1/2)arctan((1/n))−(1/(n^2 +1)))with U_0 =(√π)sin((π/4) −1)

$${we}\:{have}\:{x}^{\mathrm{2}} −\mathrm{2}{x}\:={x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{1}−\mathrm{1}\:=\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\:{changement} \\ $$$${x}−\mathrm{1}\:={t}\:{give}\:{U}_{{n}} =\int_{−\infty} ^{+\infty} \:{e}^{−{n}\left({t}+\mathrm{1}\right)^{\mathrm{2}} } {sin}\left({t}^{\mathrm{2}} −\mathrm{1}\right){dt} \\ $$$$={Im}\:\left(\int_{−\infty} ^{+\infty} \:\:{e}^{−{n}\left({t}+\mathrm{1}\right)^{\mathrm{2}} +{i}\left({t}^{\mathrm{2}} −\mathrm{1}\right)} {dt}\right)\:={Im}\left({W}_{{n}} \right) \\ $$$$\int_{−\infty} ^{+\infty} \:\:{e}^{−{n}\left({t}+\mathrm{1}\right)^{\mathrm{2}} \:+{i}\left({t}^{\mathrm{2}} −\mathrm{1}\right)} {dt}\:=\int_{−\infty} ^{+\infty} \:{e}^{−{n}\left({t}^{\mathrm{2}} \:+\mathrm{2}{t}+\mathrm{1}\right)+{it}^{\mathrm{2}} −{i}} {dt} \\ $$$$={e}^{−{i}} \:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left({n}−{i}\right){t}^{\mathrm{2}} \:−\mathrm{2}{nt}\:−{n}} {dt} \\ $$$$={e}^{−\left({n}+{i}\right)} \:\int_{−\infty} ^{+\infty} \:{e}^{−\left\{\left(\sqrt{{n}−{i}}{t}\right)^{\mathrm{2}} \:+\mathrm{2}{nt}\right\}} {dt} \\ $$$$={e}^{−\left({n}+{i}\right)} \:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left\{\:\:\left(\sqrt{{n}−{i}}{t}\right)^{\mathrm{2}} \:+\mathrm{2}\frac{{n}}{\sqrt{{n}−{i}}}\sqrt{{n}−{i}}{t}\:\:+\left(\frac{{n}}{\sqrt{{n}−{i}}}\right)^{\mathrm{2}} −\frac{{n}^{\mathrm{2}} }{{n}−{i}}\right\}} {dt} \\ $$$$={e}^{−\left({n}+{i}\right)} \:\int_{−\infty} ^{+\infty} \:{e}^{−\left\{\sqrt{{n}−{i}}{t}\:+\frac{{n}}{\sqrt{{n}−{i}}}\right\}^{\mathrm{2}} \:+\frac{{n}^{\mathrm{2}} }{{n}−{i}}} {dt}\:\:\:\left({ch}.\:\sqrt{{n}−{i}}{t}\:+\frac{{n}}{\sqrt{{n}−{i}}}\:={v}\right. \\ $$$$={e}^{\frac{{n}^{\mathrm{2}} }{{n}−{i}}−\left({n}+{i}\right)} \:\:\int_{−\infty} ^{+\infty} \:\:{e}^{−{v}^{\mathrm{2}} } \:\:\frac{{dv}}{\sqrt{{n}−{i}}}\:=\sqrt{\pi}\frac{\mathrm{1}}{\sqrt{{n}−{i}}}\:{e}^{\frac{{n}^{\mathrm{2}} −\left({n}^{\mathrm{2}} −{i}^{\mathrm{2}} \right)}{{n}−{i}}} \\ $$$$=\frac{\sqrt{\pi}}{\sqrt{{n}−{i}}}\:{e}^{−\frac{\mathrm{1}}{{n}−{i}}} \:=\frac{\sqrt{\pi}}{\sqrt{{n}−{i}}}\:{e}^{−\frac{{n}+{i}}{{n}^{\mathrm{2}} \:+\mathrm{1}}} \\ $$$${n}−{i}\:=\sqrt{\mathrm{1}+{n}^{\mathrm{2}} }\:{e}^{{i}\:{arctan}\left(\frac{−\mathrm{1}}{{n}}\right)} \:=\sqrt{\mathrm{1}+{n}^{\mathrm{2}} }{e}^{−{iarctan}\left(\frac{\mathrm{1}}{{n}}\right)} \:\Rightarrow \\ $$$$\sqrt{{n}−{i}}\:=\left(\mathrm{1}+{n}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} {e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{n}}\right)} \:\Rightarrow \\ $$$${W}_{{n}} =\sqrt{\pi}\left(\mathrm{1}+{n}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{n}}\right)} \:{e}^{−\frac{{n}}{{n}^{\mathrm{2}} \:+\mathrm{1}}} \:{e}^{−\frac{{i}}{{n}^{\mathrm{2}} \:+\mathrm{1}}} \\ $$$$=\sqrt{\pi}\left({n}^{\mathrm{2}} \:+\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{4}}} {e}^{−\frac{{n}}{{n}^{\mathrm{2}} \:+\mathrm{1}}} \:\:{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{n}}\right)−\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+\mathrm{1}}\right)} \:\Rightarrow \\ $$$${U}_{{n}} =\sqrt{\pi}\left({n}^{\mathrm{2}} \:+\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{4}}} {e}^{−\frac{{n}}{{n}^{\mathrm{2}} \:+\mathrm{1}}} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{n}}\right)−\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+\mathrm{1}}\right){with} \\ $$$${U}_{\mathrm{0}} =\sqrt{\pi}{sin}\left(\frac{\pi}{\mathrm{4}}\:−\mathrm{1}\right) \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 09/Aug/19

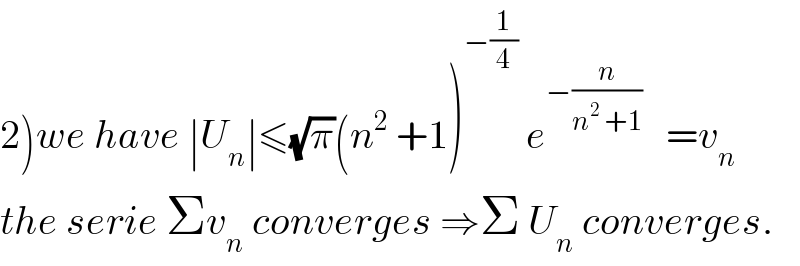
2)we have ∣U_n ∣≤(√π)(n^2 +1)^(−(1/4)) e^(−(n/(n^2 +1))) =v_n the serie Σv_n converges ⇒Σ U_n converges.

$$\left.\mathrm{2}\right){we}\:{have}\:\mid{U}_{{n}} \mid\leqslant\sqrt{\pi}\left({n}^{\mathrm{2}} \:+\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{−\frac{{n}}{{n}^{\mathrm{2}} \:+\mathrm{1}}} \:\:\:={v}_{{n}} \\ $$$${the}\:{serie}\:\Sigma{v}_{{n}} \:{converges}\:\Rightarrow\Sigma\:{U}_{{n}} \:{converges}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com