
Question Number 157989 by mnjuly1970 last updated on 30/Oct/21
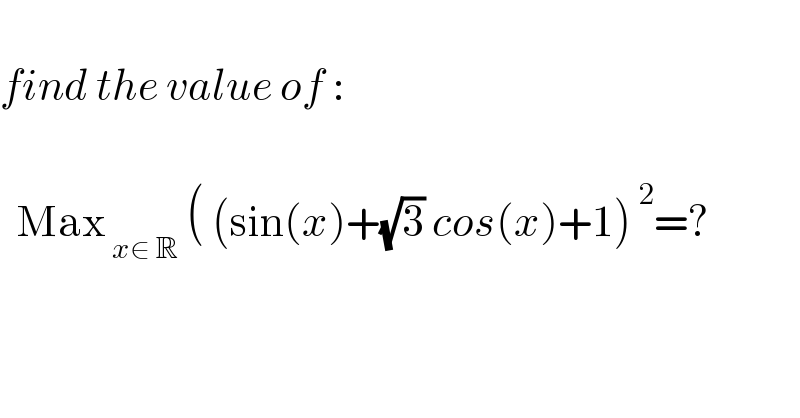
$$\: \\ $$$${find}\:{the}\:{value}\:{of}\:: \\ $$$$\: \\ $$$$\:\:\mathrm{Max}_{\:{x}\in\:\mathbb{R}} \:\left(\:\left(\mathrm{sin}\left({x}\right)+\sqrt{\mathrm{3}}\:{cos}\left({x}\right)+\mathrm{1}\right)^{\:\mathrm{2}} =?\right. \\ $$$$ \\ $$
Commented by cortano last updated on 30/Oct/21
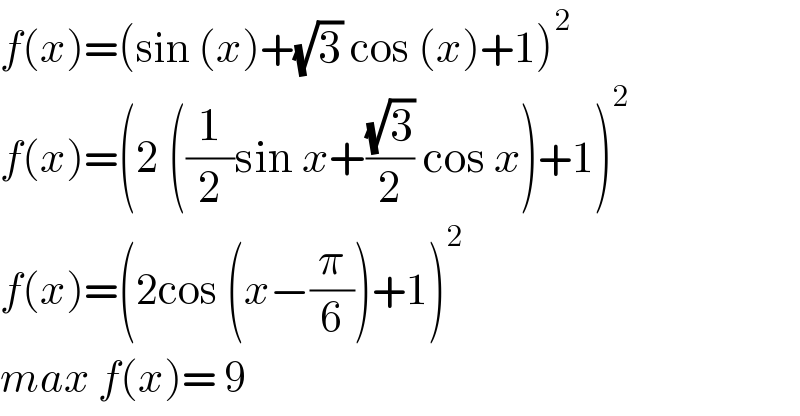
$${f}\left({x}\right)=\left(\mathrm{sin}\:\left({x}\right)+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\left({x}\right)+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${f}\left({x}\right)=\left(\mathrm{2}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:{x}\right)+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${f}\left({x}\right)=\left(\mathrm{2cos}\:\left({x}−\frac{\pi}{\mathrm{6}}\right)+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${max}\:{f}\left({x}\right)=\:\mathrm{9} \\ $$
Commented by mnjuly1970 last updated on 30/Oct/21

$${thanks}\:{alot}\:\:{sir} \\ $$
