Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 204569 by pticantor last updated on 21/Feb/24

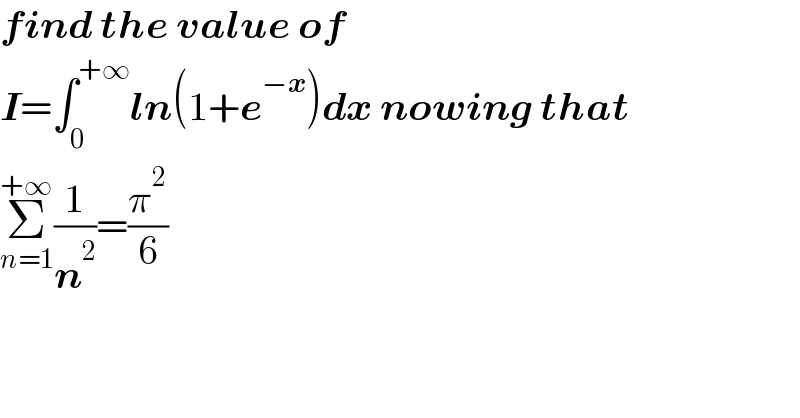
find the value of I=∫_0 ^(+∞) ln(1+e^(−x) )dx nowing that Σ_(n=1) ^(+∞) (1/n^2 )=(π^2 /6)

$$\boldsymbol{{find}}\:\boldsymbol{{the}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\: \\ $$$$\boldsymbol{{I}}=\int_{\mathrm{0}} ^{+\infty} \boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{e}}^{−\boldsymbol{{x}}} \right)\boldsymbol{{dx}}\:\boldsymbol{{nowing}}\:\boldsymbol{{that}}\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{{n}}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Answered by witcher3 last updated on 22/Feb/24

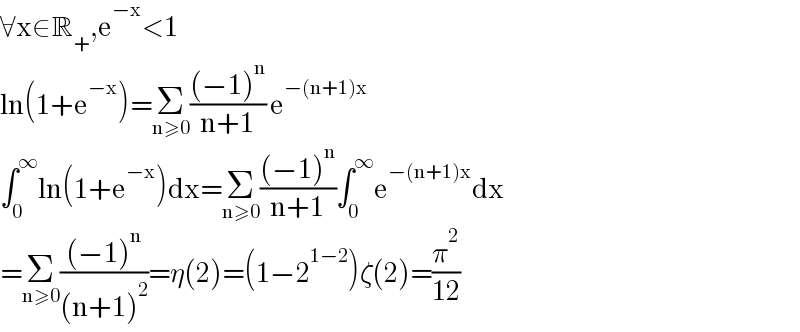
∀x∈R_+ ,e^(−x) <1 ln(1+e^(−x) )=Σ_(n≥0) (((−1)^n )/(n+1)) e^(−(n+1)x) ∫_0 ^∞ ln(1+e^(−x) )dx=Σ_(n≥0) (((−1)^n )/(n+1))∫_0 ^∞ e^(−(n+1)x) dx =Σ_(n≥0) (((−1)^n )/((n+1)^2 ))=η(2)=(1−2^(1−2) )ζ(2)=(π^2 /(12))

$$\forall\mathrm{x}\in\mathbb{R}_{+} ,\mathrm{e}^{−\mathrm{x}} <\mathrm{1} \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \: \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)\mathrm{dx}=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }=\eta\left(\mathrm{2}\right)=\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\mathrm{2}} \right)\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Commented by pticantor last updated on 23/Feb/24

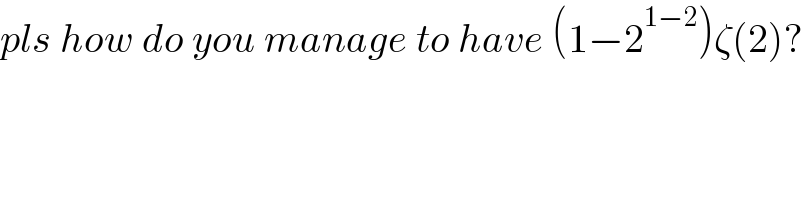
pls how do you manage to have (1−2^(1−2) )ζ(2)?

$${pls}\:{how}\:{do}\:{you}\:{manage}\:{to}\:{have}\:\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\mathrm{2}} \right)\zeta\left(\mathrm{2}\right)? \\ $$

Commented by witcher3 last updated on 23/Feb/24

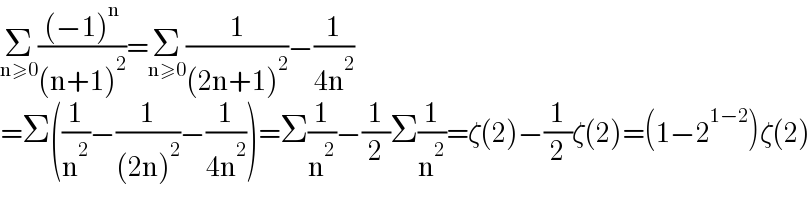
Σ_(n≥0) (((−1)^n )/((n+1)^2 ))=Σ_(n≥0) (1/((2n+1)^2 ))−(1/(4n^2 )) =Σ((1/n^2 )−(1/((2n)^2 ))−(1/(4n^2 )))=Σ(1/n^2 )−(1/2)Σ(1/n^2 )=ζ(2)−(1/2)ζ(2)=(1−2^(1−2) )ζ(2)

$$\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} } \\ $$$$=\Sigma\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{2n}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} }\right)=\Sigma\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }=\zeta\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right)=\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\mathrm{2}} \right)\zeta\left(\mathrm{2}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com