Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 29551 by abdo imad last updated on 09/Feb/18

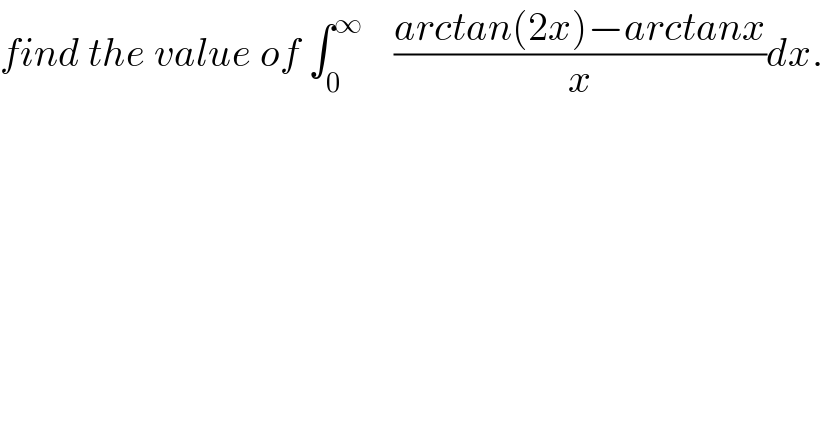
$$findthevalueof{\int }_0^{\mathrm{\infty }}\frac{arctan\left(2x\right)-arctanx}{x}dx.$$

Commented by prof Abdo imad last updated on 11/Feb/18

$$letputI={\int }_0^{\mathrm{\infty }}\frac{arctan\left(2x\right)-arctanx}{x}dxwehave$$$$I=lim{}_{\xi \to +\mathrm{\infty }}I\left(\xi \right)/I\left(\xi \right)={\int }_0^{\xi }\frac{arctan\left(2x\right)-arctanx}{x}dx$$$$={\int }_0^{\xi }\frac{arctan\left(2x\right)}{x}dx-{\int }_0^{\xi }\frac{srctanx}{x}dx$$$$={\int }_0^{2\xi }\frac{arctant}{\frac{t}{2}}\frac{dt}{2}-{\int }_0^{\xi }\frac{arctanx}{x}dx$$$$={\int }_{\xi }^{2\xi }\frac{arctanx}{x}dxbut\mathrm{\exists }c\in ]\xi ,2\xi [/$$$$I\left(\xi \right)=arctan\xi {\int }_{\xi }^{2\xi }\frac{dx}{x}=ln\left(2\right)arctan\left(\xi \right)and$$$${lim}_{\xi \to +\mathrm{\infty }}I\left(\xi \right)=\frac{\pi }{2}ln\left(2\right).\Rightarrow I=\frac{\pi }{2}ln\left(2\right).$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com