Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 31969 by abdo imad last updated on 17/Mar/18

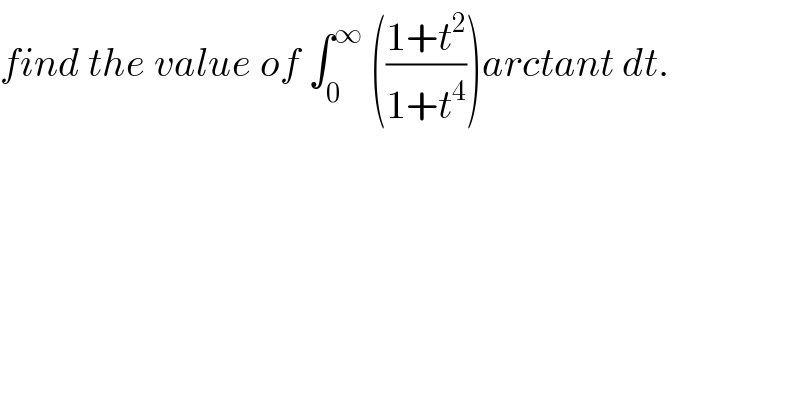
find the value of ∫_0 ^∞ (((1+t^2 )/(1+t^4 )))arctant dt.

$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\right){arctant}\:{dt}. \\ $$

Commented by abdo imad last updated on 19/Mar/18

let put I = ∫_0 ^∞ ((arctant)/(1+t^4 )) dt .ch.x=(1/t) give I = ∫_0 ^∞ (((π/2) −arctant)/(1+(1/t^4 ))) (dt/t^2 ) = ∫_0 ^∞ (((π/2) −arctant)/(t^2 +(1/t^2 ))) dt =∫_0 ^∞ ((t^2 ( (π/2) −arctant))/(1+t^4 )) dt =(π/2) ∫_0 ^∞ (t^2 /(1+t^4 ))dt −∫_0 ^∞ ((t^2 arctant)/(1+t^2 ))dt⇒ ∫_0 ^∞ (((1+t^2 )/(1+t^4 )))arctant dt = (π/2) ∫_0 ^∞ (t^2 /(1+t^4 )) dt .ch.t^4 =u give ∫_0 ^∞ (t^2 /(1+t^4 )) dt = ∫_0 ^∞ (((u^(1/4) )^2 )/(1+u)) (1/4) u^((1/4)−1) du =(1/4) ∫_0 ^∞ (u^((1/2) +(1/4)−1) /(1+u)) du =(1/4) ∫_0 ^∞ (u^((3/4) −1) /(1+u)) du =(1/4) (π/(sin(((3π)/4)))) =(π/4) (1/(1/(√2))) =((π(√2))/4) ⇒ ∫_0 ^∞ (((1+t^2 )/(1+t^4 )))arctantdt = (π/2) ((π(√2))/4) =(π^2 /8) (√2) . I have used the result ∫_0 ^∞ (t^(a−1) /(1+t))dt=(π/(sin(πa))) with 0<a<1

$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{arctant}}{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt}\:\:\:\:.{ch}.{x}=\frac{\mathrm{1}}{{t}}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{\frac{\pi}{\mathrm{2}}\:−{arctant}}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{4}} }}\:\frac{{dt}}{{t}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\frac{\pi}{\mathrm{2}}\:−{arctant}}{{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{\mathrm{2}} \left(\:\frac{\pi}{\mathrm{2}}\:−{arctant}\right)}{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt}\:=\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt}\:−\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\mathrm{2}} \:{arctant}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\right){arctant}\:{dt}\:=\:\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt}\:\:.{ch}.{t}^{\mathrm{4}} \:={u}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\left({u}^{\frac{\mathrm{1}}{\mathrm{4}}} \right)^{\mathrm{2}} }{\mathrm{1}+{u}}\:\frac{\mathrm{1}}{\mathrm{4}}\:{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{u}}\:{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{\frac{\mathrm{3}}{\mathrm{4}}\:−\mathrm{1}} }{\mathrm{1}+{u}}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}}\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\right){arctantdt}\:=\:\frac{\pi}{\mathrm{2}}\:\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\sqrt{\mathrm{2}}\:. \\ $$$${I}\:{have}\:{used}\:{the}\:{result}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}=\frac{\pi}{{sin}\left(\pi{a}\right)}\:{with}\:\mathrm{0}<{a}<\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com