Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 209670 by mokys last updated on 18/Jul/24

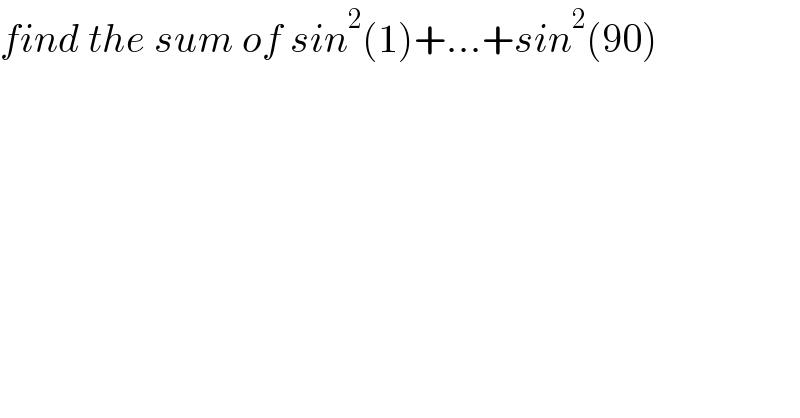
find the sum of sin^2 (1)+...+sin^2 (90)

$${find}\:{the}\:{sum}\:{of}\:{sin}^{\mathrm{2}} \left(\mathrm{1}\right)+...+{sin}^{\mathrm{2}} \left(\mathrm{90}\right) \\ $$

Answered by Ar Brandon last updated on 18/Jul/24

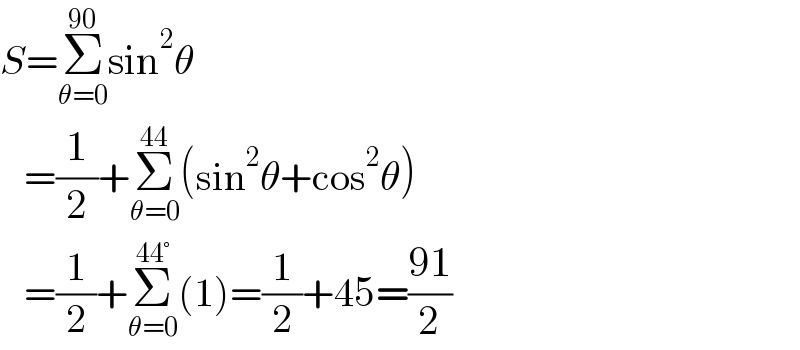
S=Σ_(θ=0) ^(90) sin^2 θ =(1/2)+Σ_(θ=0) ^(44) (sin^2 θ+cos^2 θ) =(1/2)+Σ_(θ=0) ^(44°) (1)=(1/2)+45=((91)/2)

$${S}=\underset{\theta=\mathrm{0}} {\overset{\mathrm{90}} {\sum}}\mathrm{sin}^{\mathrm{2}} \theta \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}+\underset{\theta=\mathrm{0}} {\overset{\mathrm{44}} {\sum}}\left(\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}+\underset{\theta=\mathrm{0}} {\overset{\mathrm{44}°} {\sum}}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{45}=\frac{\mathrm{91}}{\mathrm{2}} \\ $$

Commented by mokys last updated on 18/Jul/24

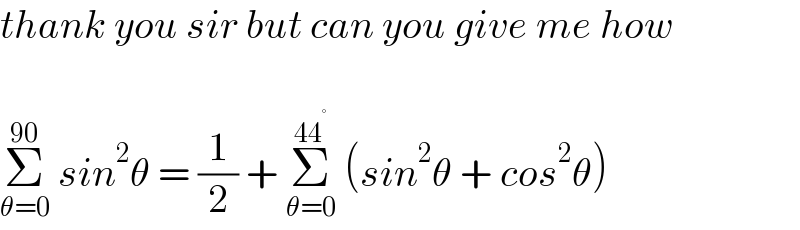
thank you sir but can you give me how Σ_(θ=0) ^(90) sin^2 θ = (1/2) + Σ_(θ=0) ^(44^° ) (sin^2 θ + cos^2 θ)

$${thank}\:{you}\:{sir}\:{but}\:{can}\:{you}\:{give}\:{me}\:{how}\: \\ $$$$ \\ $$$$\underset{\theta=\mathrm{0}} {\overset{\mathrm{90}} {\sum}}\:{sin}^{\mathrm{2}} \theta\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\underset{\theta=\mathrm{0}} {\overset{\mathrm{44}^{°} } {\sum}}\:\left({sin}^{\mathrm{2}} \theta\:+\:{cos}^{\mathrm{2}} \theta\right)\: \\ $$

Commented by Ar Brandon last updated on 18/Jul/24

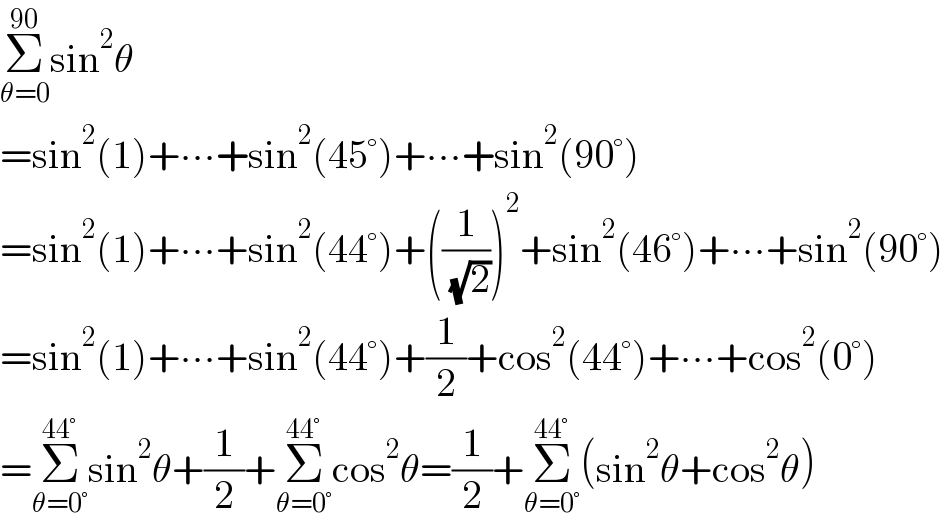
Σ_(θ=0) ^(90) sin^2 θ =sin^2 (1)+∙∙∙+sin^2 (45°)+∙∙∙+sin^2 (90°) =sin^2 (1)+∙∙∙+sin^2 (44°)+((1/( (√2))))^2 +sin^2 (46°)+∙∙∙+sin^2 (90°) =sin^2 (1)+∙∙∙+sin^2 (44°)+(1/2)+cos^2 (44°)+∙∙∙+cos^2 (0°) =Σ_(θ=0°) ^(44°) sin^2 θ+(1/2)+Σ_(θ=0°) ^(44°) cos^2 θ=(1/2)+Σ_(θ=0°) ^(44°) (sin^2 θ+cos^2 θ)

$$\underset{\theta=\mathrm{0}} {\overset{\mathrm{90}} {\sum}}\mathrm{sin}^{\mathrm{2}} \theta \\ $$$$=\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)+\centerdot\centerdot\centerdot+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{45}°\right)+\centerdot\centerdot\centerdot+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}°\right) \\ $$$$=\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)+\centerdot\centerdot\centerdot+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{44}°\right)+\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \left(\mathrm{46}°\right)+\centerdot\centerdot\centerdot+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}°\right) \\ $$$$=\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)+\centerdot\centerdot\centerdot+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{44}°\right)+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{44}°\right)+\centerdot\centerdot\centerdot+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{0}°\right) \\ $$$$=\underset{\theta=\mathrm{0}°} {\overset{\mathrm{44}°} {\sum}}\mathrm{sin}^{\mathrm{2}} \theta+\frac{\mathrm{1}}{\mathrm{2}}+\underset{\theta=\mathrm{0}°} {\overset{\mathrm{44}°} {\sum}}\mathrm{cos}^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\mathrm{2}}+\underset{\theta=\mathrm{0}°} {\overset{\mathrm{44}°} {\sum}}\left(\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta\right) \\ $$

Answered by Sutrisno last updated on 18/Jul/24

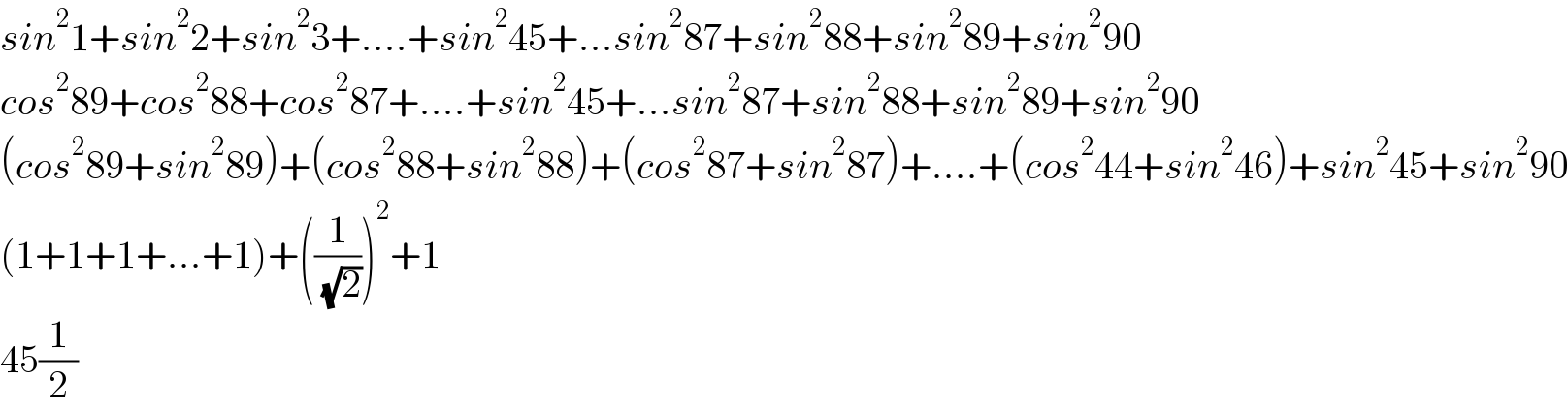
sin^2 1+sin^2 2+sin^2 3+....+sin^2 45+...sin^2 87+sin^2 88+sin^2 89+sin^2 90 cos^2 89+cos^2 88+cos^2 87+....+sin^2 45+...sin^2 87+sin^2 88+sin^2 89+sin^2 90 (cos^2 89+sin^2 89)+(cos^2 88+sin^2 88)+(cos^2 87+sin^2 87)+....+(cos^2 44+sin^2 46)+sin^2 45+sin^2 90 (1+1+1+...+1)+((1/( (√2))))^2 +1 45(1/2)

$${sin}^{\mathrm{2}} \mathrm{1}+{sin}^{\mathrm{2}} \mathrm{2}+{sin}^{\mathrm{2}} \mathrm{3}+....+{sin}^{\mathrm{2}} \mathrm{45}+...{sin}^{\mathrm{2}} \mathrm{87}+{sin}^{\mathrm{2}} \mathrm{88}+{sin}^{\mathrm{2}} \mathrm{89}+{sin}^{\mathrm{2}} \mathrm{90} \\ $$$${cos}^{\mathrm{2}} \mathrm{89}+{cos}^{\mathrm{2}} \mathrm{88}+{cos}^{\mathrm{2}} \mathrm{87}+....+{sin}^{\mathrm{2}} \mathrm{45}+...{sin}^{\mathrm{2}} \mathrm{87}+{sin}^{\mathrm{2}} \mathrm{88}+{sin}^{\mathrm{2}} \mathrm{89}+{sin}^{\mathrm{2}} \mathrm{90} \\ $$$$\left({cos}^{\mathrm{2}} \mathrm{89}+{sin}^{\mathrm{2}} \mathrm{89}\right)+\left({cos}^{\mathrm{2}} \mathrm{88}+{sin}^{\mathrm{2}} \mathrm{88}\right)+\left({cos}^{\mathrm{2}} \mathrm{87}+{sin}^{\mathrm{2}} \mathrm{87}\right)+....+\left({cos}^{\mathrm{2}} \mathrm{44}+{sin}^{\mathrm{2}} \mathrm{46}\right)+{sin}^{\mathrm{2}} \mathrm{45}+{sin}^{\mathrm{2}} \mathrm{90} \\ $$$$\left(\mathrm{1}+\mathrm{1}+\mathrm{1}+...+\mathrm{1}\right)+\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{45}\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com