
Question Number 165262 by mkam last updated on 28/Jan/22
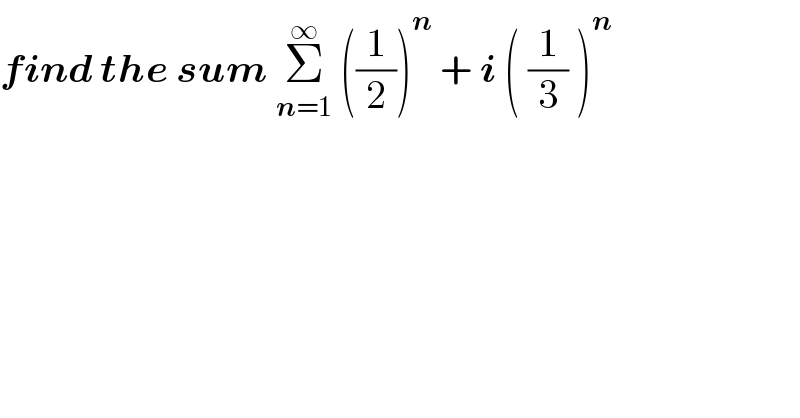
$$\boldsymbol{{find}}\:\boldsymbol{{the}}\:\boldsymbol{{sum}}\:\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\boldsymbol{{n}}} \:+\:\boldsymbol{{i}}\:\left(\:\frac{\mathrm{1}}{\mathrm{3}}\:\right)^{\boldsymbol{{n}}} \: \\ $$
Answered by Mathspace last updated on 28/Jan/22
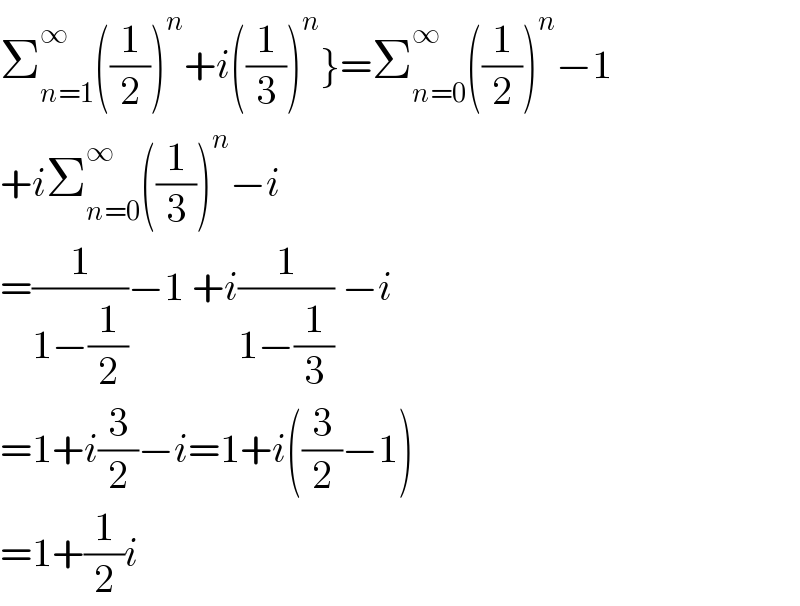
$$\left.\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +{i}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \right\}=\sum_{{n}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} −\mathrm{1} \\ $$$$+{i}\sum_{{n}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} −{i} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}−\mathrm{1}\:+{i}\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\:−{i} \\ $$$$=\mathrm{1}+{i}\frac{\mathrm{3}}{\mathrm{2}}−{i}=\mathrm{1}+{i}\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{i} \\ $$
Answered by Ar Brandon last updated on 28/Jan/22
![S=Σ_(n=1) ^∞ [((1/2))^n +i((1/3))^n ] =Σ_(n=1) ^∞ ((1/2))^n +iΣ_(n=1) ^∞ ((1/3))^n =1+i(1/2)](Q165263.png)
$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +{i}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \right] \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +{i}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} \\ $$$$\:\:\:=\mathrm{1}+{i}\frac{\mathrm{1}}{\mathrm{2}} \\ $$
