
Question Number 78335 by john santu last updated on 16/Jan/20
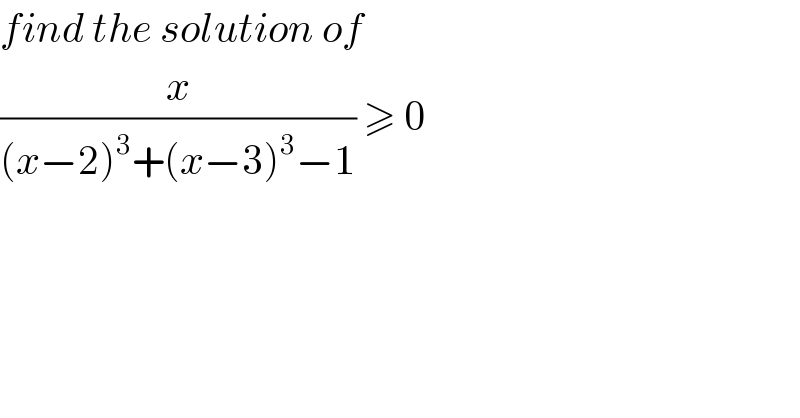
$${find}\:{the}\:{solution}\:{of} \\ $$$$\frac{{x}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{3}} −\mathrm{1}}\:\geqslant\:\mathrm{0} \\ $$
Answered by MJS last updated on 16/Jan/20
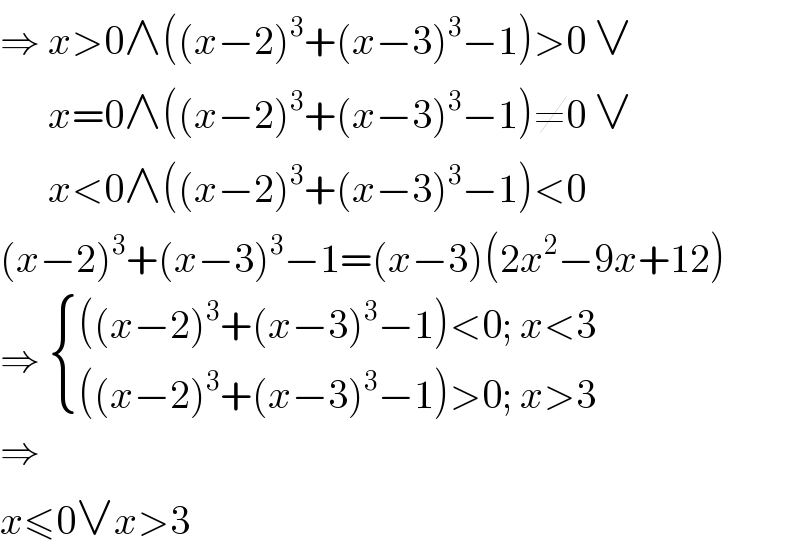
$$\Rightarrow\:{x}>\mathrm{0}\wedge\left(\left({x}−\mathrm{2}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{3}} −\mathrm{1}\right)>\mathrm{0}\:\vee \\ $$$$\:\:\:\:\:\:{x}=\mathrm{0}\wedge\left(\left({x}−\mathrm{2}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{3}} −\mathrm{1}\right)\neq\mathrm{0}\:\vee \\ $$$$\:\:\:\:\:\:{x}<\mathrm{0}\wedge\left(\left({x}−\mathrm{2}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{3}} −\mathrm{1}\right)<\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{3}} −\mathrm{1}=\left({x}−\mathrm{3}\right)\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{12}\right) \\ $$$$\Rightarrow\:\begin{cases}{\left(\left({x}−\mathrm{2}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{3}} −\mathrm{1}\right)<\mathrm{0};\:{x}<\mathrm{3}}\\{\left(\left({x}−\mathrm{2}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{3}} −\mathrm{1}\right)>\mathrm{0};\:{x}>\mathrm{3}}\end{cases} \\ $$$$\Rightarrow \\ $$$${x}\leqslant\mathrm{0}\vee{x}>\mathrm{3} \\ $$
Commented by john santu last updated on 16/Jan/20

$${thanks}\:{sir} \\ $$
