Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 63534 by Rio Michael last updated on 05/Jul/19

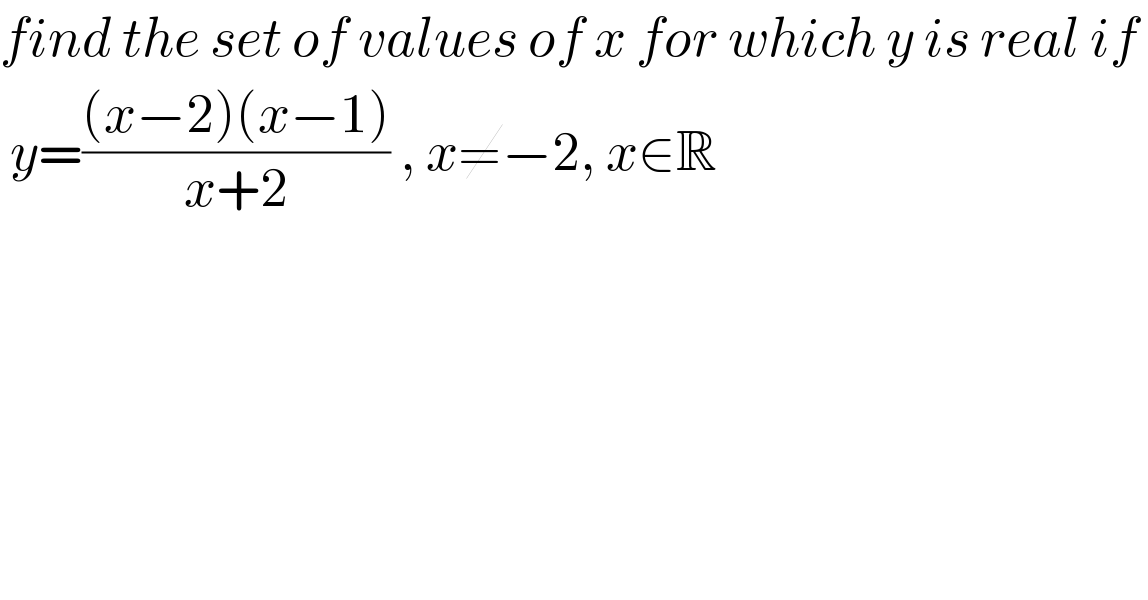
find the set of values of x for which y is real if y=(((x−2)(x−1))/(x+2)) , x≠−2, x∈R

$${find}\:{the}\:{set}\:{of}\:{values}\:{of}\:{x}\:{for}\:{which}\:{y}\:{is}\:{real}\:{if}\: \\ $$$$\:{y}=\frac{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)}{{x}+\mathrm{2}}\:,\:{x}\neq−\mathrm{2},\:{x}\in\mathbb{R} \\ $$

Answered by MJS last updated on 05/Jul/19

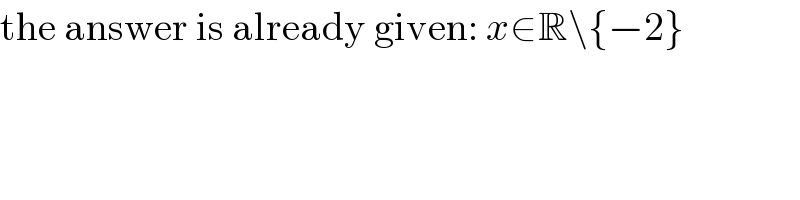
the answer is already given: x∈R\{−2}

$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{already}\:\mathrm{given}:\:{x}\in\mathbb{R}\backslash\left\{−\mathrm{2}\right\} \\ $$

Commented by Rio Michael last updated on 05/Jul/19

why is it so?

$${why}\:{is}\:{it}\:{so}? \\ $$

Commented by Prithwish sen last updated on 05/Jul/19

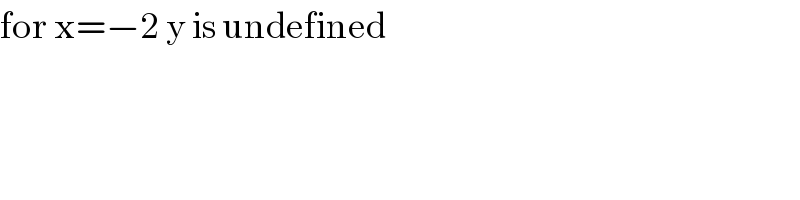
for x=−2 y is undefined

$$\mathrm{for}\:\mathrm{x}=−\mathrm{2}\:\mathrm{y}\:\mathrm{is}\:\mathrm{undefined} \\ $$

Commented by MJS last updated on 05/Jul/19

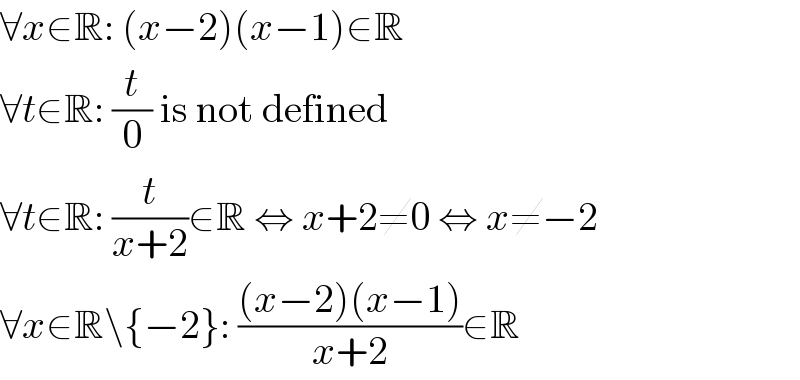
∀x∈R: (x−2)(x−1)∈R ∀t∈R: (t/0) is not defined ∀t∈R: (t/(x+2))∈R ⇔ x+2≠0 ⇔ x≠−2 ∀x∈R\{−2}: (((x−2)(x−1))/(x+2))∈R

$$\forall{x}\in\mathbb{R}:\:\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)\in\mathbb{R} \\ $$$$\forall{t}\in\mathbb{R}:\:\frac{{t}}{\mathrm{0}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined} \\ $$$$\forall{t}\in\mathbb{R}:\:\frac{{t}}{{x}+\mathrm{2}}\in\mathbb{R}\:\Leftrightarrow\:{x}+\mathrm{2}\neq\mathrm{0}\:\Leftrightarrow\:{x}\neq−\mathrm{2} \\ $$$$\forall{x}\in\mathbb{R}\backslash\left\{−\mathrm{2}\right\}:\:\frac{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)}{{x}+\mathrm{2}}\in\mathbb{R} \\ $$

Commented by Rio Michael last updated on 11/Jul/19

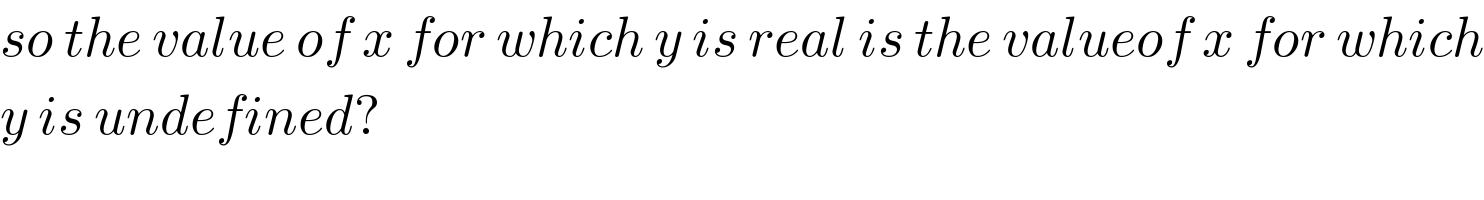
so the value of x for which y is real is the valueof x for which y is undefined?

$${so}\:{the}\:{value}\:{of}\:{x}\:{for}\:{which}\:{y}\:{is}\:{real}\:{is}\:{the}\:{valueof}\:{x}\:{for}\:{which} \\ $$$${y}\:{is}\:{undefined}? \\ $$

Commented by MJS last updated on 12/Jul/19

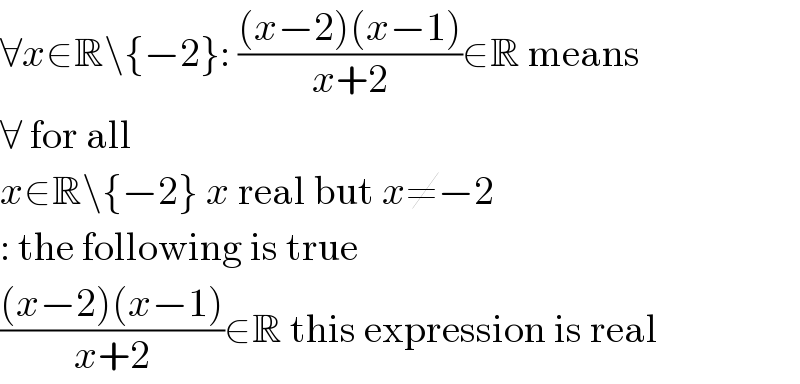
∀x∈R\{−2}: (((x−2)(x−1))/(x+2))∈R means ∀ for all x∈R\{−2} x real but x≠−2 : the following is true (((x−2)(x−1))/(x+2))∈R this expression is real

$$\forall{x}\in\mathbb{R}\backslash\left\{−\mathrm{2}\right\}:\:\frac{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)}{{x}+\mathrm{2}}\in\mathbb{R}\:\mathrm{means} \\ $$$$\forall\:\mathrm{for}\:\mathrm{all} \\ $$$${x}\in\mathbb{R}\backslash\left\{−\mathrm{2}\right\}\:{x}\:\mathrm{real}\:\mathrm{but}\:{x}\neq−\mathrm{2} \\ $$$$:\:\mathrm{the}\:\mathrm{following}\:\mathrm{is}\:\mathrm{true} \\ $$$$\frac{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)}{{x}+\mathrm{2}}\in\mathbb{R}\:\mathrm{this}\:\mathrm{expression}\:\mathrm{is}\:\mathrm{real} \\ $$

Commented by Rio Michael last updated on 12/Jul/19

i get it now.

$${i}\:{get}\:{it}\:{now}. \\ $$

Commented by Rio Michael last updated on 12/Jul/19

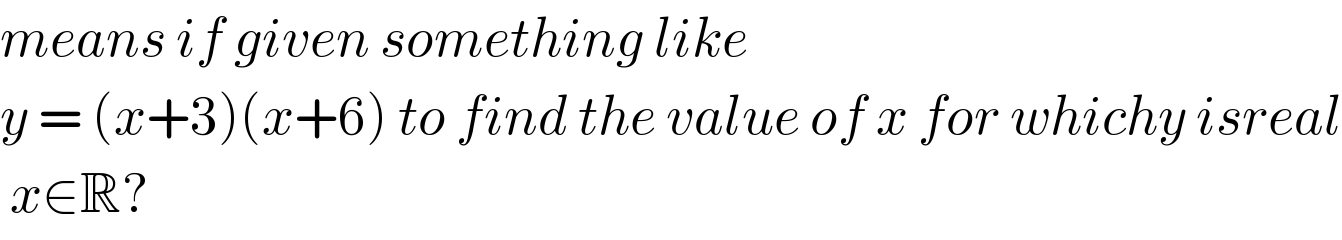
means if given something like y = (x+3)(x+6) to find the value of x for whichy isreal x∈R?

$${means}\:{if}\:{given}\:{something}\:{like} \\ $$$${y}\:=\:\left({x}+\mathrm{3}\right)\left({x}+\mathrm{6}\right)\:{to}\:{find}\:{the}\:{value}\:{of}\:{x}\:{for}\:{whichy}\:{isreal} \\ $$$$\:{x}\in\mathbb{R}? \\ $$

Commented by MJS last updated on 12/Jul/19

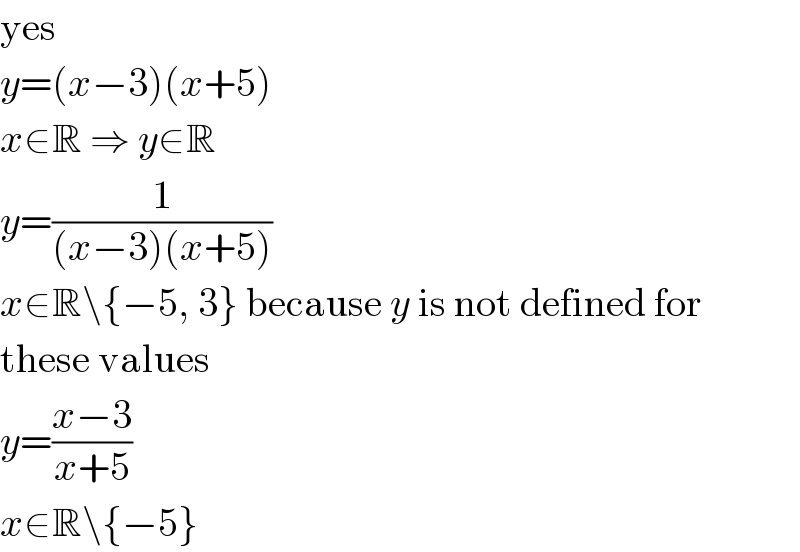
yes y=(x−3)(x+5) x∈R ⇒ y∈R y=(1/((x−3)(x+5))) x∈R\{−5, 3} because y is not defined for these values y=((x−3)/(x+5)) x∈R\{−5}

$$\mathrm{yes} \\ $$$${y}=\left({x}−\mathrm{3}\right)\left({x}+\mathrm{5}\right) \\ $$$${x}\in\mathbb{R}\:\Rightarrow\:{y}\in\mathbb{R} \\ $$$${y}=\frac{\mathrm{1}}{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{5}\right)} \\ $$$${x}\in\mathbb{R}\backslash\left\{−\mathrm{5},\:\mathrm{3}\right\}\:\mathrm{because}\:{y}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for} \\ $$$$\mathrm{these}\:\mathrm{values} \\ $$$${y}=\frac{{x}−\mathrm{3}}{{x}+\mathrm{5}} \\ $$$${x}\in\mathbb{R}\backslash\left\{−\mathrm{5}\right\} \\ $$

Commented by Rio Michael last updated on 12/Jul/19

thanks so much

$${thanks}\:{so}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com