
Question Number 190284 by cortano12 last updated on 31/Mar/23

$$\mathrm{find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{if}\:\mathrm{4}^{\mathrm{2023}} \: \\ $$$$\mathrm{divides}\:\mathrm{by}\:\mathrm{7} \\ $$
Answered by alcohol last updated on 31/Mar/23
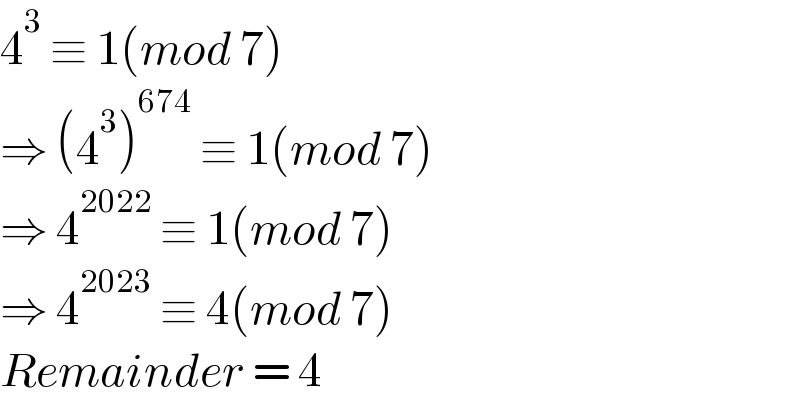
$$\mathrm{4}^{\mathrm{3}} \:\equiv\:\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow\:\left(\mathrm{4}^{\mathrm{3}} \right)^{\mathrm{674}} \:\equiv\:\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow\:\mathrm{4}^{\mathrm{2022}} \:\equiv\:\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow\:\mathrm{4}^{\mathrm{2023}} \:\equiv\:\mathrm{4}\left({mod}\:\mathrm{7}\right) \\ $$$${Remainder}\:=\:\mathrm{4} \\ $$
Answered by BaliramKumar last updated on 31/Mar/23
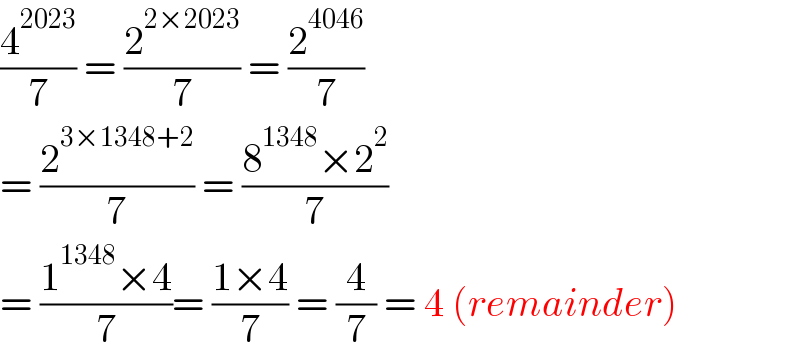
$$\frac{\mathrm{4}^{\mathrm{2023}} }{\mathrm{7}}\:=\:\frac{\mathrm{2}^{\mathrm{2}×\mathrm{2023}} }{\mathrm{7}}\:=\:\frac{\mathrm{2}^{\mathrm{4046}} }{\mathrm{7}}\: \\ $$$$=\:\frac{\mathrm{2}^{\mathrm{3}×\mathrm{1348}+\mathrm{2}} }{\mathrm{7}}\:=\:\frac{\mathrm{8}^{\mathrm{1348}} ×\mathrm{2}^{\mathrm{2}} }{\mathrm{7}} \\ $$$$=\:\frac{\mathrm{1}^{\mathrm{1348}} ×\mathrm{4}}{\mathrm{7}}=\:\frac{\mathrm{1}×\mathrm{4}}{\mathrm{7}}\:=\:\frac{\mathrm{4}}{\mathrm{7}}\:=\:\mathrm{4}\:\left({remainder}\right) \\ $$
