
Question Number 50551 by pooja24 last updated on 17/Dec/18
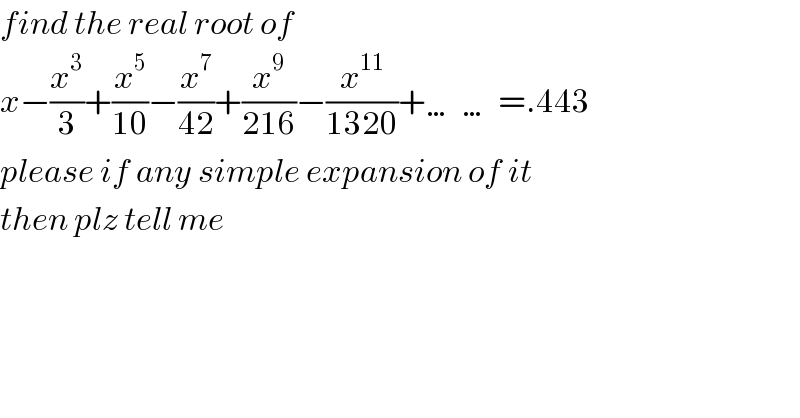
$${find}\:{the}\:{real}\:{root}\:{of} \\ $$$${x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{10}}−\frac{{x}^{\mathrm{7}} }{\mathrm{42}}+\frac{{x}^{\mathrm{9}} }{\mathrm{216}}−\frac{{x}^{\mathrm{11}} }{\mathrm{1320}}+\ldots\ldots=.\mathrm{443} \\ $$$${please}\:{if}\:{any}\:{simple}\:{expansion}\:{of}\:{it} \\ $$$${then}\:{plz}\:{tell}\:{me} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18

$${f}\left({x}\right)={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{10}}−\frac{{x}^{\mathrm{7}} }{\mathrm{42}}+\frac{{x}^{\mathrm{9}} }{\mathrm{216}}−\frac{{x}^{\mathrm{11}} }{\mathrm{1320}}+... \\ $$$$\frac{{df}\left({x}\right)}{{dx}}=\mathrm{1}−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{2}}−\frac{{x}^{\mathrm{6}} }{\mathrm{6}}+\frac{{x}^{\mathrm{8}} }{\mathrm{24}}−\frac{{x}^{\mathrm{10}} }{\mathrm{120}}+... \\ $$$${let}={k}={x}^{\mathrm{2}} \\ $$$${Right}\:{hand}\:{side} \\ $$$$\mathrm{1}−{k}+\frac{{k}^{\mathrm{2}} }{\mathrm{2}!}−\frac{{k}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{k}^{\mathrm{4}} }{\mathrm{4}!}−\frac{{k}^{\mathrm{5}} }{\mathrm{5}!}+... \\ $$$$={e}^{−{k}} \\ $$$$={e}^{−{x}^{\mathrm{2}} } \\ $$$${so}\:\frac{{df}\left({x}\right)}{{dx}}={e}^{−{x}^{\mathrm{2}} } \\ $$$${f}\left({x}\right)=\int{e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$$ \\ $$$$\:\:\:\:\:\left[{from}\:\:{table}\:{e}^{−\mathrm{0}.\mathrm{812}} \approx\mathrm{0}.\mathrm{443}\right. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
