
Question Number 203329 by Calculusboy last updated on 16/Jan/24
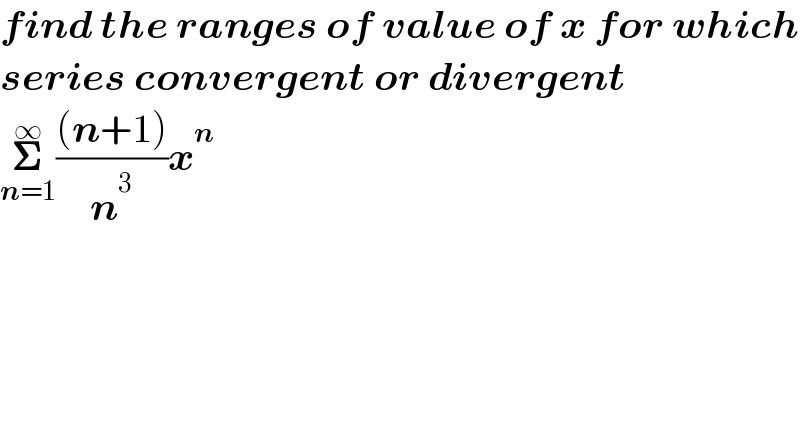
$$\boldsymbol{{find}}\:\boldsymbol{{the}}\:\boldsymbol{{ranges}}\:\boldsymbol{{of}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\:\boldsymbol{{x}}\:\boldsymbol{{for}}\:\boldsymbol{{which}}\: \\ $$$$\boldsymbol{{series}}\:\boldsymbol{{convergent}}\:\boldsymbol{{or}}\:\boldsymbol{{divergent}} \\ $$$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\boldsymbol{{n}}^{\mathrm{3}} }\boldsymbol{{x}}^{\boldsymbol{{n}}} \\ $$
Answered by Mathspace last updated on 17/Jan/24
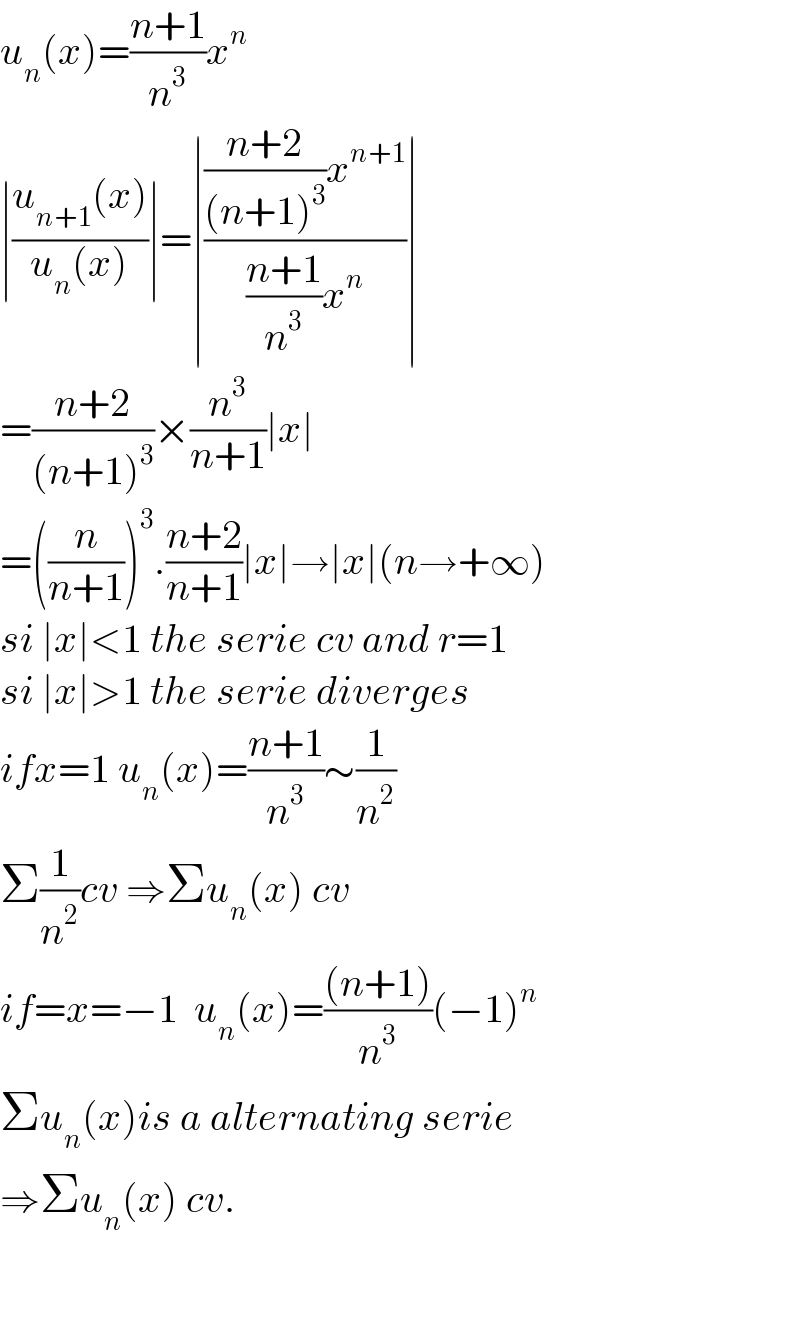
$${u}_{{n}} \left({x}\right)=\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }{x}^{{n}} \\ $$$$\mid\frac{{u}_{{n}+\mathrm{1}} \left({x}\right)}{{u}_{{n}} \left({x}\right)}\mid=\mid\frac{\frac{{n}+\mathrm{2}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} }{x}^{{n}+\mathrm{1}} }{\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }{x}^{{n}} }\mid \\ $$$$=\frac{{n}+\mathrm{2}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} }×\frac{{n}^{\mathrm{3}} }{{n}+\mathrm{1}}\mid{x}\mid \\ $$$$=\left(\frac{{n}}{{n}+\mathrm{1}}\right)^{\mathrm{3}} .\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}\mid{x}\mid\rightarrow\mid{x}\mid\left({n}\rightarrow+\infty\right) \\ $$$${si}\:\mid{x}\mid<\mathrm{1}\:{the}\:{serie}\:{cv}\:{and}\:{r}=\mathrm{1} \\ $$$${si}\:\mid{x}\mid>\mathrm{1}\:{the}\:{serie}\:{diverges} \\ $$$${ifx}=\mathrm{1}\:{u}_{{n}} \left({x}\right)=\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} }\sim\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$\Sigma\frac{\mathrm{1}}{{n}^{\mathrm{2}} }{cv}\:\Rightarrow\Sigma{u}_{{n}} \left({x}\right)\:{cv} \\ $$$${if}={x}=−\mathrm{1}\:\:{u}_{{n}} \left({x}\right)=\frac{\left({n}+\mathrm{1}\right)}{{n}^{\mathrm{3}} }\left(−\mathrm{1}\right)^{{n}} \\ $$$$\Sigma{u}_{{n}} \left({x}\right){is}\:{a}\:{alternating}\:{serie} \\ $$$$\Rightarrow\Sigma{u}_{{n}} \left({x}\right)\:{cv}. \\ $$$$ \\ $$
Commented by Calculusboy last updated on 17/Jan/24

$$\boldsymbol{{nice}}\:\boldsymbol{{sir}} \\ $$
