
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 176501 by infinityaction last updated on 20/Sep/22
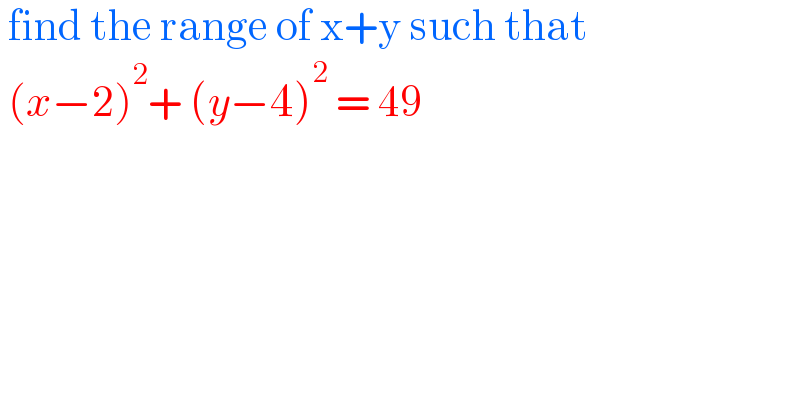
Commented by cortano1 last updated on 20/Sep/22
![let x+y=k ⇒x+y−k=0 is tangent to circle so 7=((∣2+4−k∣)/( (√2))) ⇒∣k−6∣ = 7(√2) ⇒−7(√2) ≤ k−6≤7(√2) ⇒6−7(√2) ≤k≤6+7(√2) Therefore range of x+y is [ 6−7(√2) , 6+7(√2) ]](Q176504.png)
Answered by Peace last updated on 20/Sep/22
![{ ((x=2+7cos(t))),((y=4+7sin(t))) :}t∈[0,2π[ x+y=6+7(sin(t)+cos(t))=6+7(√2)(sin(t+(π/4))) x+y∈[6−7(√2),6+7(√2)]](Q176529.png)
