Question and Answers Forum

All Questions      Topic List

Vector Calculus Questions

Previous in All Question      Next in All Question      

Previous in Vector Calculus      Next in Vector Calculus      

Question Number 110320 by bemath last updated on 28/Aug/20

find the point of intersection of the line r^→ =(1−2t,3+4t,t) and the plane 3x−2y+5z=15

$${find}\:{the}\:{point}\:{of}\:{intersection} \\ $$$${of}\:{the}\:{line}\:\overset{\rightarrow} {{r}}=\left(\mathrm{1}−\mathrm{2}{t},\mathrm{3}+\mathrm{4}{t},{t}\right) \\ $$$${and}\:{the}\:{plane}\:\mathrm{3}{x}−\mathrm{2}{y}+\mathrm{5}{z}=\mathrm{15}\: \\ $$

Answered by mr W last updated on 28/Aug/20

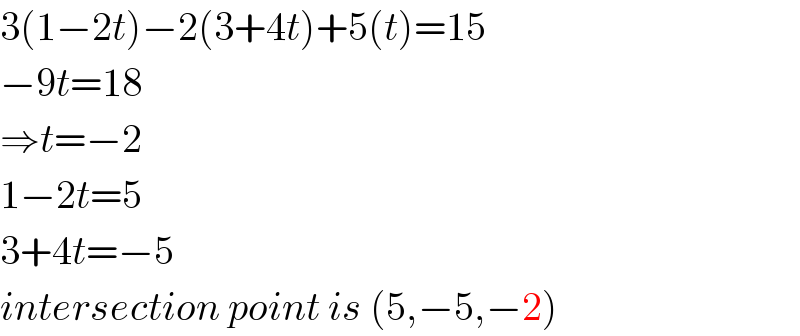
3(1−2t)−2(3+4t)+5(t)=15 −9t=18 ⇒t=−2 1−2t=5 3+4t=−5 intersection point is (5,−5,−2)

$$\mathrm{3}\left(\mathrm{1}−\mathrm{2}{t}\right)−\mathrm{2}\left(\mathrm{3}+\mathrm{4}{t}\right)+\mathrm{5}\left({t}\right)=\mathrm{15} \\ $$$$−\mathrm{9}{t}=\mathrm{18} \\ $$$$\Rightarrow{t}=−\mathrm{2} \\ $$$$\mathrm{1}−\mathrm{2}{t}=\mathrm{5} \\ $$$$\mathrm{3}+\mathrm{4}{t}=−\mathrm{5} \\ $$$${intersection}\:{point}\:{is}\:\left(\mathrm{5},−\mathrm{5},−\mathrm{2}\right) \\ $$

Commented by I want to learn more last updated on 28/Aug/20

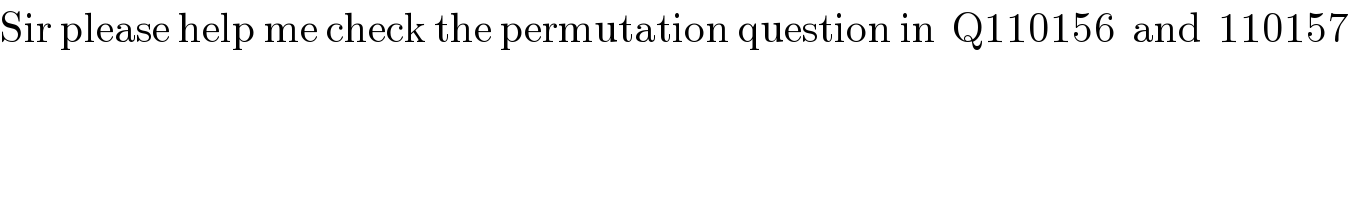
Sir please help me check the permutation question in Q110156 and 110157

$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{check}\:\mathrm{the}\:\mathrm{permutation}\:\mathrm{question}\:\mathrm{in}\:\:\mathrm{Q110156}\:\:\mathrm{and}\:\:\mathrm{110157} \\ $$

Answered by Rio Michael last updated on 28/Aug/20

x = 1−2t y = 3 + 4t z = t substituting ⇒ 3(1−2t)−2(3 + 4t) + 5t = 15 3−6t−6−8t + 5t = 15 ⇒ −9t = 18 hence t = −2 ⇒ point of intersection is (5,−5,−2)

$${x}\:=\:\mathrm{1}−\mathrm{2}{t} \\ $$$${y}\:=\:\mathrm{3}\:+\:\mathrm{4}{t} \\ $$$${z}\:=\:{t} \\ $$$$\mathrm{substituting}\:\Rightarrow\:\mathrm{3}\left(\mathrm{1}−\mathrm{2}{t}\right)−\mathrm{2}\left(\mathrm{3}\:+\:\mathrm{4}{t}\right)\:+\:\mathrm{5}{t}\:=\:\mathrm{15} \\ $$$$\mathrm{3}−\mathrm{6}{t}−\mathrm{6}−\mathrm{8}{t}\:+\:\mathrm{5}{t}\:=\:\mathrm{15} \\ $$$$\Rightarrow\:−\mathrm{9}{t}\:=\:\mathrm{18}\:\mathrm{hence}\:{t}\:=\:−\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{point}\:\mathrm{of}\:\mathrm{intersection}\:\mathrm{is}\:\:\left(\mathrm{5},−\mathrm{5},−\mathrm{2}\right) \\ $$

Answered by 1549442205PVT last updated on 28/Aug/20

The equation of the line is { ((x=1−2t)),((y=3+4t)),((z=t)) :} Replace into 3x−2y+5z=15 we have 3(1−2t)−2(3+4t)+5t=15 ⇔−9t=18⇒t=−2 Substituting into the system above we get x=5,y=−5,−2 Therefore,the intersection point of the line and the plane is the point M(5,−5,−2)

$$\mathrm{The}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{is}\:\begin{cases}{\mathrm{x}=\mathrm{1}−\mathrm{2t}}\\{\mathrm{y}=\mathrm{3}+\mathrm{4t}}\\{\mathrm{z}=\mathrm{t}}\end{cases} \\ $$$$\mathrm{Replace}\:\mathrm{into}\:\mathrm{3}{x}−\mathrm{2}{y}+\mathrm{5}{z}=\mathrm{15}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{3}\left(\mathrm{1}−\mathrm{2t}\right)−\mathrm{2}\left(\mathrm{3}+\mathrm{4t}\right)+\mathrm{5t}=\mathrm{15} \\ $$$$\Leftrightarrow−\mathrm{9t}=\mathrm{18}\Rightarrow\mathrm{t}=−\mathrm{2} \\ $$$$\mathrm{Substituting}\:\mathrm{into}\:\mathrm{the}\:\mathrm{system}\:\mathrm{above} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{x}=\mathrm{5},\mathrm{y}=−\mathrm{5},−\mathrm{2} \\ $$$$\mathrm{Therefore},\mathrm{the}\:\mathrm{intersection}\:\mathrm{point}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{line}\:\mathrm{and}\:\mathrm{the}\:\mathrm{plane}\:\mathrm{is}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{M}\left(\mathrm{5},−\mathrm{5},−\mathrm{2}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com