
Question Number 130197 by mohammad17 last updated on 23/Jan/21
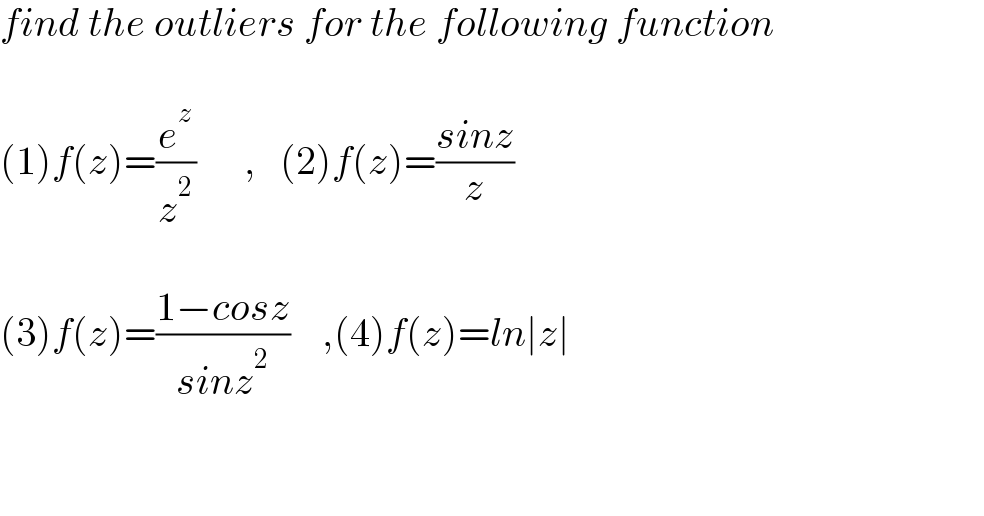
$${find}\:{the}\:{outliers}\:{for}\:{the}\:{following}\:{function} \\ $$$$ \\ $$$$\left(\mathrm{1}\right){f}\left({z}\right)=\frac{{e}^{{z}} }{{z}^{\mathrm{2}} }\:\:\:\:\:\:,\:\:\:\left(\mathrm{2}\right){f}\left({z}\right)=\frac{{sinz}}{{z}} \\ $$$$ \\ $$$$\left(\mathrm{3}\right){f}\left({z}\right)=\frac{\mathrm{1}−{cosz}}{{sinz}^{\mathrm{2}} }\:\:\:\:,\left(\mathrm{4}\right){f}\left({z}\right)={ln}\mid{z}\mid \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 23/Jan/21
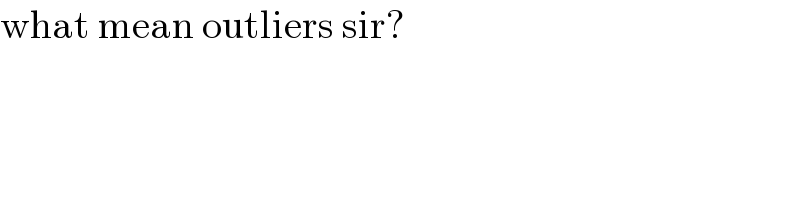
$$\mathrm{what}\:\mathrm{mean}\:\mathrm{outliers}\:\mathrm{sir}? \\ $$
Commented by mohammad17 last updated on 23/Jan/21
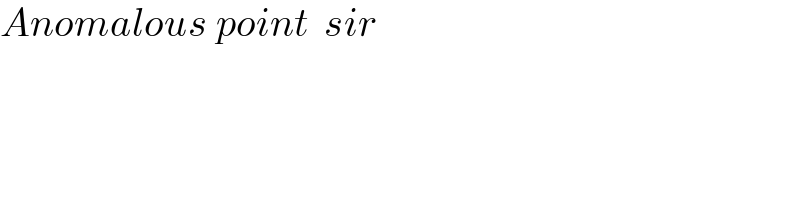
$${Anomalous}\:{point}\:\:{sir} \\ $$
Commented by mohammad17 last updated on 23/Jan/21

$$????? \\ $$
