Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 216074 by CrispyXYZ last updated on 27/Jan/25

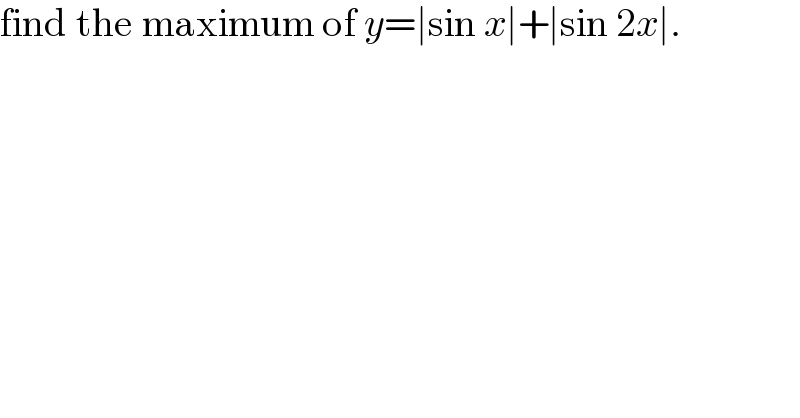
find the maximum of y=∣sin x∣+∣sin 2x∣.

$$\mathrm{find}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{of}\:{y}=\mid\mathrm{sin}\:{x}\mid+\mid\mathrm{sin}\:\mathrm{2}{x}\mid. \\ $$

Answered by efronzo1 last updated on 27/Jan/25

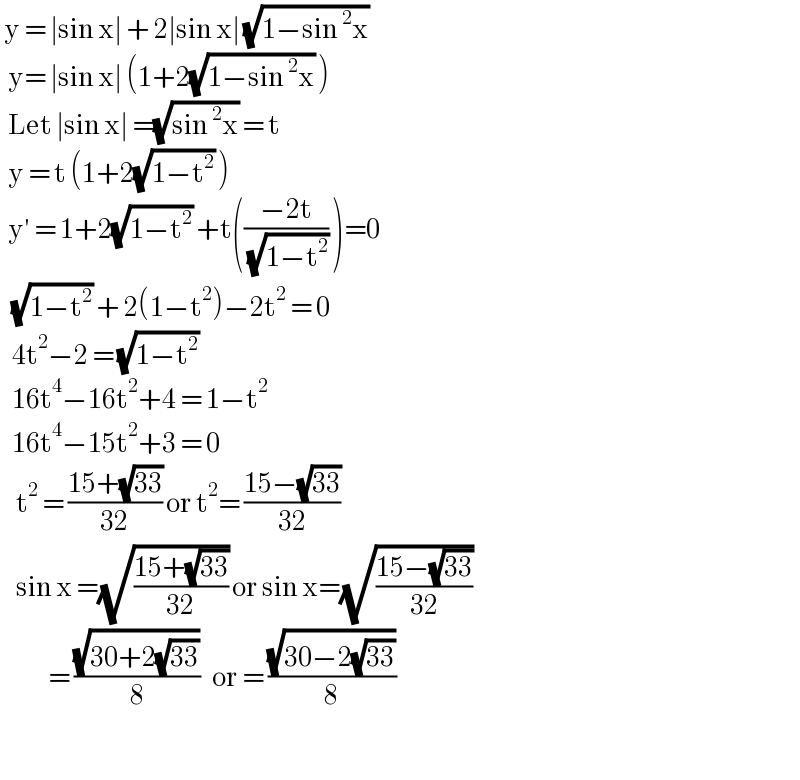
y = ∣sin x∣ + 2∣sin x∣ (√(1−sin^2 x)) y= ∣sin x∣ (1+2(√(1−sin^2 x)) ) Let ∣sin x∣ =(√(sin^2 x)) = t y = t (1+2(√(1−t^2 )) ) y′ = 1+2(√(1−t^2 )) +t(((−2t)/( (√(1−t^2 )))) )=0 (√(1−t^2 )) + 2(1−t^2 )−2t^2 = 0 4t^2 −2 = (√(1−t^2 )) 16t^4 −16t^2 +4 = 1−t^2 16t^4 −15t^2 +3 = 0 t^2 = ((15+(√(33)))/(32)) or t^2 = ((15−(√(33)))/(32)) sin x =(√((15+(√(33)))/(32))) or sin x=(√((15−(√(33)))/(32))) = ((√(30+2(√(33))))/8) or = ((√(30−2(√(33))))/8)

$$\:\mathrm{y}\:=\:\mid\mathrm{sin}\:\mathrm{x}\mid\:+\:\mathrm{2}\mid\mathrm{sin}\:\mathrm{x}\mid\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\mathrm{y}=\:\mid\mathrm{sin}\:\mathrm{x}\mid\:\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:\right) \\ $$$$\:\:\mathrm{Let}\:\mid\mathrm{sin}\:\mathrm{x}\mid\:=\sqrt{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:=\:\mathrm{t}\: \\ $$$$\:\:\mathrm{y}\:=\:\mathrm{t}\:\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:\right) \\ $$$$\:\:\mathrm{y}'\:=\:\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:+\mathrm{t}\left(\frac{−\mathrm{2t}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:\right)=\mathrm{0} \\ $$$$\:\:\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:+\:\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)−\mathrm{2t}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\:\:\:\mathrm{4t}^{\mathrm{2}} −\mathrm{2}\:=\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} } \\ $$$$\:\:\:\mathrm{16t}^{\mathrm{4}} −\mathrm{16t}^{\mathrm{2}} +\mathrm{4}\:=\:\mathrm{1}−\mathrm{t}^{\mathrm{2}} \\ $$$$\:\:\:\mathrm{16t}^{\mathrm{4}} −\mathrm{15t}^{\mathrm{2}} +\mathrm{3}\:=\:\mathrm{0}\: \\ $$$$\:\:\:\:\mathrm{t}^{\mathrm{2}} \:=\:\frac{\mathrm{15}+\sqrt{\mathrm{33}}}{\mathrm{32}}\:\mathrm{or}\:\mathrm{t}^{\mathrm{2}} =\:\frac{\mathrm{15}−\sqrt{\mathrm{33}}}{\mathrm{32}} \\ $$$$\:\:\:\:\mathrm{sin}\:\mathrm{x}\:=\sqrt{\frac{\mathrm{15}+\sqrt{\mathrm{33}}}{\mathrm{32}}}\:\mathrm{or}\:\mathrm{sin}\:\mathrm{x}=\sqrt{\frac{\mathrm{15}−\sqrt{\mathrm{33}}}{\mathrm{32}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{30}+\mathrm{2}\sqrt{\mathrm{33}}}}{\mathrm{8}}\:\:\:\mathrm{or}\:=\:\frac{\sqrt{\mathrm{30}−\mathrm{2}\sqrt{\mathrm{33}}}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$

Answered by Frix last updated on 27/Jan/25

y=∣sin x∣+∣sin 2x∣ is periodic and symmetric It′s enough to look at the interval [0, (π/2)] where y=sin x +sin 2x y′=0 ⇒ cos^2 x +((cos x)/4)−(1/2)=0 cos x =−(1/8)±((√(33))/8) 0≤x≤(π/2) ⇒ x=cos^(−1) (−(1/8)+((√(33))/8)) y_(max) =((√(6(69+11(√(33))))/(16))≈1.76017259

$${y}=\mid\mathrm{sin}\:{x}\mid+\mid\mathrm{sin}\:\mathrm{2}{x}\mid\:\mathrm{is}\:\mathrm{periodic}\:\mathrm{and}\:\mathrm{symmetric} \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{enough}\:\mathrm{to}\:\mathrm{look}\:\mathrm{at}\:\mathrm{the}\:\mathrm{interval}\:\left[\mathrm{0},\:\frac{\pi}{\mathrm{2}}\right] \\ $$$$\mathrm{where}\:{y}=\mathrm{sin}\:{x}\:+\mathrm{sin}\:\mathrm{2}{x} \\ $$$${y}'=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:+\frac{\mathrm{cos}\:{x}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{cos}\:{x}\:=−\frac{\mathrm{1}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{33}}}{\mathrm{8}} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}\:\Rightarrow\:{x}=\mathrm{cos}^{−\mathrm{1}} \:\left(−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\sqrt{\mathrm{33}}}{\mathrm{8}}\right) \\ $$$${y}_{\mathrm{max}} =\frac{\sqrt{\mathrm{6}\left(\mathrm{69}+\mathrm{11}\sqrt{\mathrm{33}}\right.}}{\mathrm{16}}\approx\mathrm{1}.\mathrm{76017259} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com