
Question Number 212201 by universe last updated on 06/Oct/24
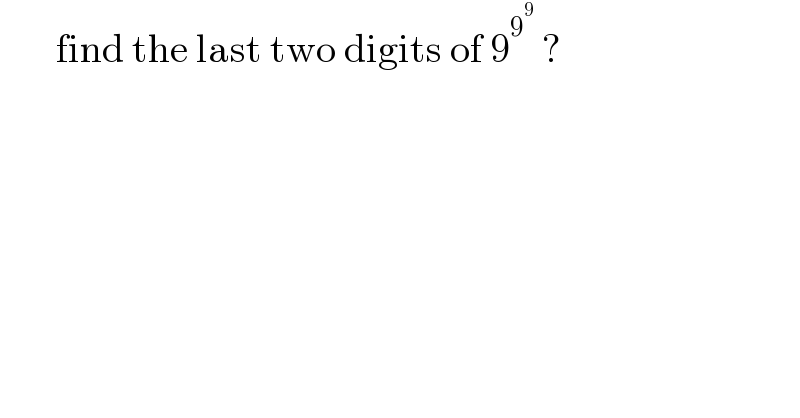
$$\:\:\:\:\:\:\:\mathrm{find}\:\mathrm{the}\:\mathrm{last}\:\mathrm{two}\:\mathrm{digits}\:\mathrm{of}\:\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \:? \\ $$
Answered by A5T last updated on 06/Oct/24
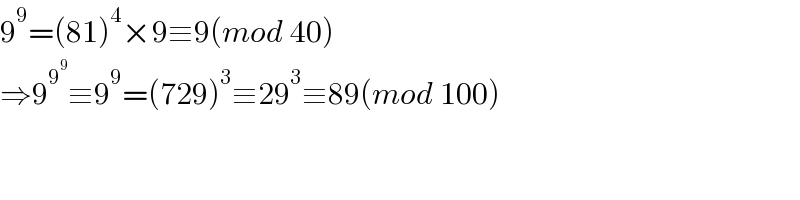
$$\mathrm{9}^{\mathrm{9}} =\left(\mathrm{81}\right)^{\mathrm{4}} ×\mathrm{9}\equiv\mathrm{9}\left({mod}\:\mathrm{40}\right) \\ $$$$\Rightarrow\mathrm{9}^{\mathrm{9}^{\mathrm{9}} } \equiv\mathrm{9}^{\mathrm{9}} =\left(\mathrm{729}\right)^{\mathrm{3}} \equiv\mathrm{29}^{\mathrm{3}} \equiv\mathrm{89}\left({mod}\:\mathrm{100}\right) \\ $$
