Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 191846 by malwan last updated on 01/May/23

find the last three digits of 4^2^(42) Mohammed Alwan

$${find}\:{the}\:{last}\:{three}\:{digits} \\ $$$${of}\:\mathrm{4}^{\mathrm{2}^{\mathrm{42}} } \\ $$$${Mohammed}\:{Alwan} \\ $$

Answered by deleteduser1 last updated on 01/May/23

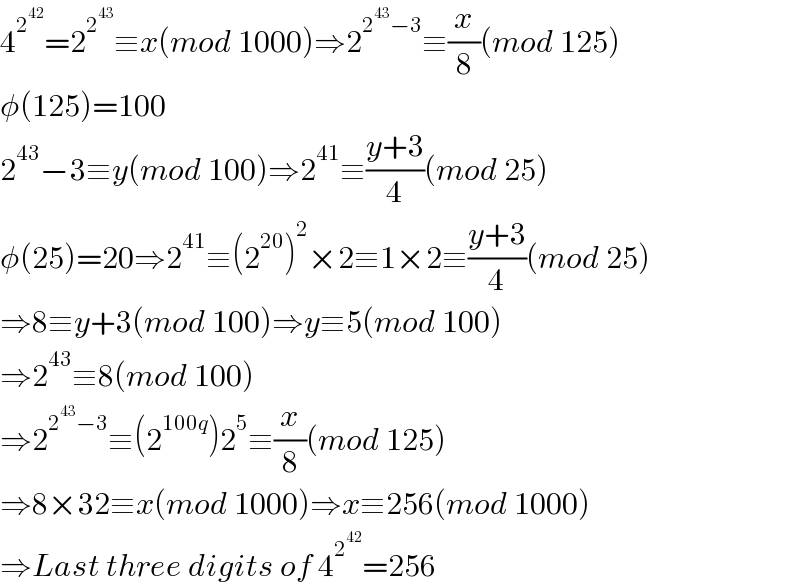
4^2^(42) =2^2^(43) ≡x(mod 1000)⇒2^(2^(43) −3) ≡(x/8)(mod 125) φ(125)=100 2^(43) −3≡y(mod 100)⇒2^(41) ≡((y+3)/4)(mod 25) φ(25)=20⇒2^(41) ≡(2^(20) )^2 ×2≡1×2≡((y+3)/4)(mod 25) ⇒8≡y+3(mod 100)⇒y≡5(mod 100) ⇒2^(43) ≡8(mod 100) ⇒2^(2^(43) −3) ≡(2^(100q) )2^5 ≡(x/8)(mod 125) ⇒8×32≡x(mod 1000)⇒x≡256(mod 1000) ⇒Last three digits of 4^2^(42) =256

$$\mathrm{4}^{\mathrm{2}^{\mathrm{42}} } =\mathrm{2}^{\mathrm{2}^{\mathrm{43}} } \equiv{x}\left({mod}\:\mathrm{1000}\right)\Rightarrow\mathrm{2}^{\mathrm{2}^{\mathrm{43}} −\mathrm{3}} \equiv\frac{{x}}{\mathrm{8}}\left({mod}\:\mathrm{125}\right) \\ $$$$\phi\left(\mathrm{125}\right)=\mathrm{100} \\ $$$$\mathrm{2}^{\mathrm{43}} −\mathrm{3}\equiv{y}\left({mod}\:\mathrm{100}\right)\Rightarrow\mathrm{2}^{\mathrm{41}} \equiv\frac{{y}+\mathrm{3}}{\mathrm{4}}\left({mod}\:\mathrm{25}\right) \\ $$$$\phi\left(\mathrm{25}\right)=\mathrm{20}\Rightarrow\mathrm{2}^{\mathrm{41}} \equiv\left(\mathrm{2}^{\mathrm{20}} \right)^{\mathrm{2}} ×\mathrm{2}\equiv\mathrm{1}×\mathrm{2}\equiv\frac{{y}+\mathrm{3}}{\mathrm{4}}\left({mod}\:\mathrm{25}\right) \\ $$$$\Rightarrow\mathrm{8}\equiv{y}+\mathrm{3}\left({mod}\:\mathrm{100}\right)\Rightarrow{y}\equiv\mathrm{5}\left({mod}\:\mathrm{100}\right) \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{43}} \equiv\mathrm{8}\left({mod}\:\mathrm{100}\right) \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{2}^{\mathrm{43}} −\mathrm{3}} \equiv\left(\mathrm{2}^{\mathrm{100}{q}} \right)\mathrm{2}^{\mathrm{5}} \equiv\frac{{x}}{\mathrm{8}}\left({mod}\:\mathrm{125}\right) \\ $$$$\Rightarrow\mathrm{8}×\mathrm{32}\equiv{x}\left({mod}\:\mathrm{1000}\right)\Rightarrow{x}\equiv\mathrm{256}\left({mod}\:\mathrm{1000}\right) \\ $$$$\Rightarrow{Last}\:{three}\:{digits}\:{of}\:\mathrm{4}^{\mathrm{2}^{\mathrm{42}} } =\mathrm{256} \\ $$

Commented by malwan last updated on 01/May/23

thank you so much sir

$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com