Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 203192 by MrGHK last updated on 12/Jan/24

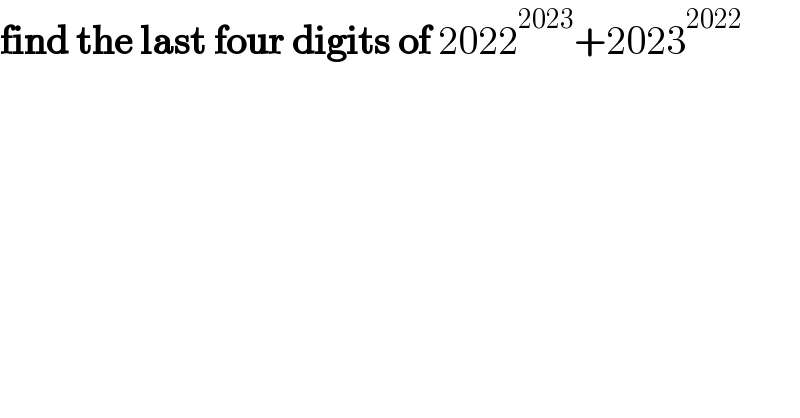
find the last four digits of 2022^(2023) +2023^(2022)

$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{last}}\:\boldsymbol{\mathrm{four}}\:\boldsymbol{\mathrm{digits}}\:\boldsymbol{\mathrm{of}}\:\mathrm{2022}^{\mathrm{2023}} +\mathrm{2023}^{\mathrm{2022}} \\ $$

Answered by deleteduser1 last updated on 12/Jan/24

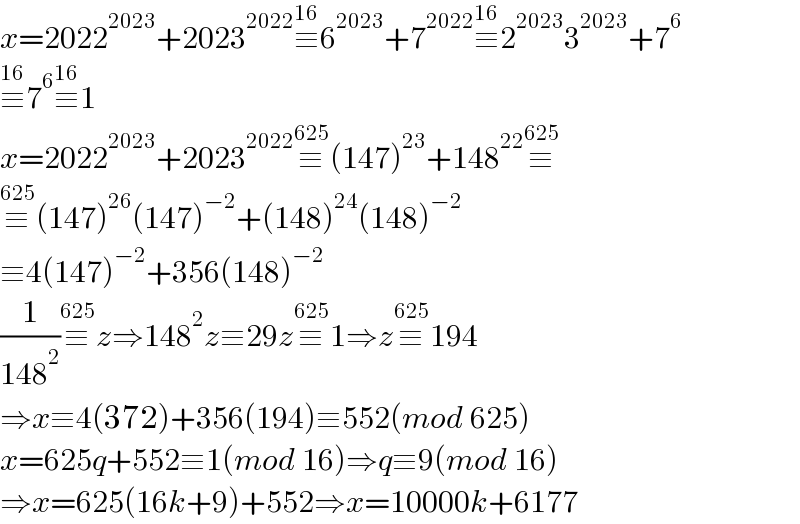
x=2022^(2023) +2023^(2022) ≡^(16) 6^(2023) +7^(2022) ≡^(16) 2^(2023) 3^(2023) +7^6 ≡^(16) 7^6 ≡^(16) 1 x=2022^(2023) +2023^(2022) ≡^(625) (147)^(23) +148^(22) ≡^(625) ≡^(625) (147)^(26) (147)^(−2) +(148)^(24) (148)^(−2) ≡4(147)^(−2) +356(148)^(−2) (1/(148^2 ))≡^(625) z⇒148^2 z≡29z≡^(625) 1⇒z≡^(625) 194 ⇒x≡4(372)+356(194)≡552(mod 625) x=625q+552≡1(mod 16)⇒q≡9(mod 16) ⇒x=625(16k+9)+552⇒x=10000k+6177

$${x}=\mathrm{2022}^{\mathrm{2023}} +\mathrm{2023}^{\mathrm{2022}} \overset{\mathrm{16}} {\equiv}\mathrm{6}^{\mathrm{2023}} +\mathrm{7}^{\mathrm{2022}} \overset{\mathrm{16}} {\equiv}\mathrm{2}^{\mathrm{2023}} \mathrm{3}^{\mathrm{2023}} +\mathrm{7}^{\mathrm{6}} \\ $$$$\overset{\mathrm{16}} {\equiv}\mathrm{7}^{\mathrm{6}} \overset{\mathrm{16}} {\equiv}\mathrm{1} \\ $$$${x}=\mathrm{2022}^{\mathrm{2023}} +\mathrm{2023}^{\mathrm{2022}} \overset{\mathrm{625}} {\equiv}\left(\mathrm{147}\right)^{\mathrm{23}} +\mathrm{148}^{\mathrm{22}} \overset{\mathrm{625}} {\equiv} \\ $$$$\overset{\mathrm{625}} {\equiv}\left(\mathrm{147}\right)^{\mathrm{26}} \left(\mathrm{147}\right)^{−\mathrm{2}} +\left(\mathrm{148}\right)^{\mathrm{24}} \left(\mathrm{148}\right)^{−\mathrm{2}} \\ $$$$\equiv\mathrm{4}\left(\mathrm{147}\right)^{−\mathrm{2}} +\mathrm{356}\left(\mathrm{148}\right)^{−\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{148}^{\mathrm{2}} }\overset{\mathrm{625}} {\equiv}{z}\Rightarrow\mathrm{148}^{\mathrm{2}} {z}\equiv\mathrm{29}{z}\overset{\mathrm{625}} {\equiv}\mathrm{1}\Rightarrow{z}\overset{\mathrm{625}} {\equiv}\mathrm{194} \\ $$$$\Rightarrow{x}\equiv\mathrm{4}\left(\mathrm{372}\right)+\mathrm{356}\left(\mathrm{194}\right)\equiv\mathrm{552}\left({mod}\:\mathrm{625}\right) \\ $$$${x}=\mathrm{625}{q}+\mathrm{552}\equiv\mathrm{1}\left({mod}\:\mathrm{16}\right)\Rightarrow{q}\equiv\mathrm{9}\left({mod}\:\mathrm{16}\right) \\ $$$$\Rightarrow{x}=\mathrm{625}\left(\mathrm{16}{k}+\mathrm{9}\right)+\mathrm{552}\Rightarrow{x}=\mathrm{10000}{k}+\mathrm{6177} \\ $$

Commented by MrGHK last updated on 13/Jan/24

thanks

$${thanks} \\ $$

Commented by MathematicalUser2357 last updated on 15/Jan/24

q+552 read the blue one

$${q}+\mathrm{552} \\ $$$${read}\:{the}\:{blue}\:{one} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com