
Question Number 214002 by RoseAli last updated on 24/Nov/24
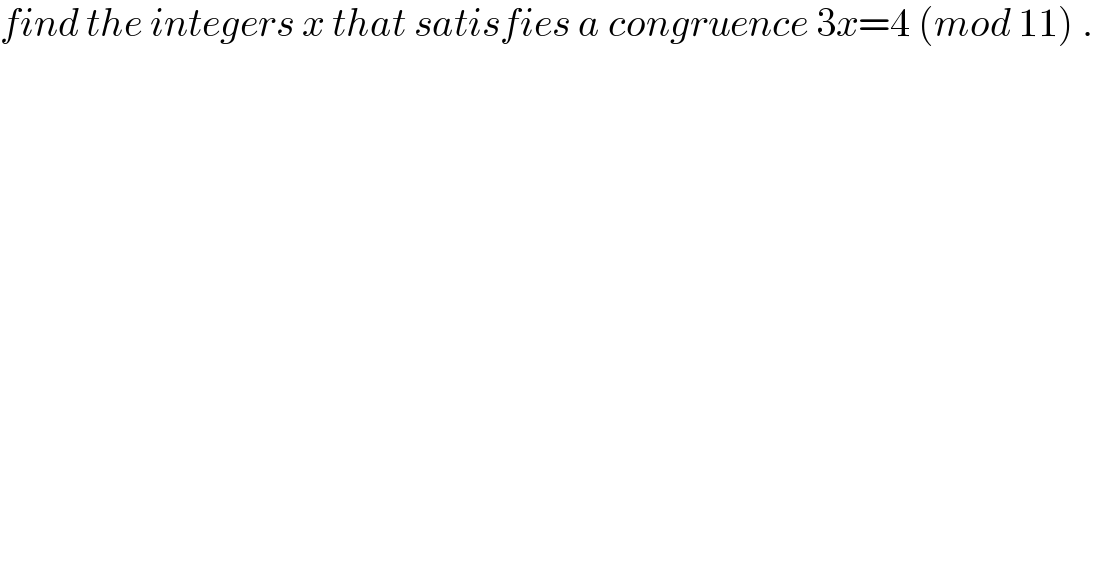
$${find}\:{the}\:{integers}\:{x}\:{that}\:{satisfies}\:{a}\:{congruence}\:\mathrm{3}{x}=\mathrm{4}\:\left({mod}\:\mathrm{11}\right)\:. \\ $$
Answered by Rasheed.Sindhi last updated on 24/Nov/24
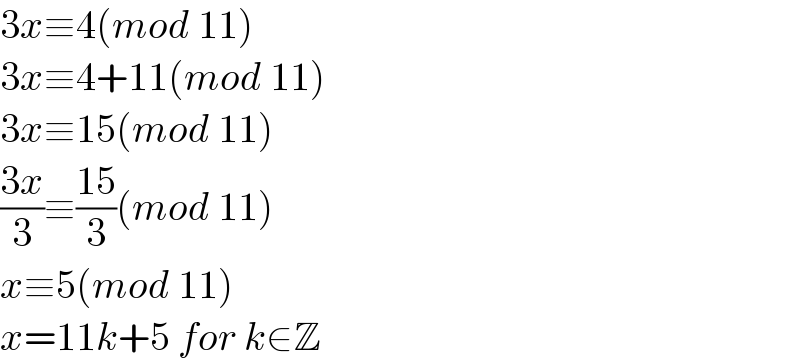
$$\mathrm{3}{x}\equiv\mathrm{4}\left({mod}\:\mathrm{11}\right) \\ $$$$\mathrm{3}{x}\equiv\mathrm{4}+\mathrm{11}\left({mod}\:\mathrm{11}\right) \\ $$$$\mathrm{3}{x}\equiv\mathrm{15}\left({mod}\:\mathrm{11}\right) \\ $$$$\frac{\mathrm{3}{x}}{\mathrm{3}}\equiv\frac{\mathrm{15}}{\mathrm{3}}\left({mod}\:\mathrm{11}\right) \\ $$$${x}\equiv\mathrm{5}\left({mod}\:\mathrm{11}\right) \\ $$$${x}=\mathrm{11}{k}+\mathrm{5}\:{for}\:{k}\in\mathbb{Z} \\ $$
Answered by mehdee7396 last updated on 24/Nov/24
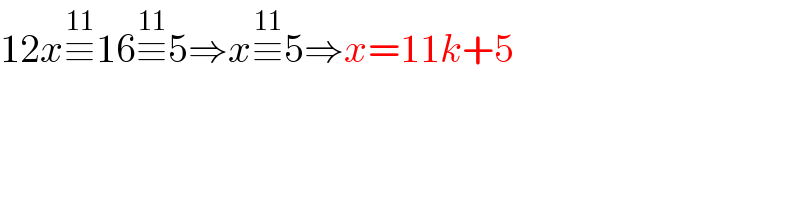
$$\mathrm{12}{x}\overset{\mathrm{11}} {\equiv}\mathrm{16}\overset{\mathrm{11}} {\equiv}\mathrm{5}\Rightarrow{x}\overset{\mathrm{11}} {\equiv}\mathrm{5}\Rightarrow{x}=\mathrm{11}{k}+\mathrm{5} \\ $$
