
Question Number 63693 by Rio Michael last updated on 07/Jul/19

$${find}\:{the}\:{general}\:{solution}\:{for}\: \\ $$$$\:{sin}\mathrm{5}\theta+{sin}\mathrm{3}\theta=\:\mathrm{1} \\ $$
Commented by Prithwish sen last updated on 07/Jul/19
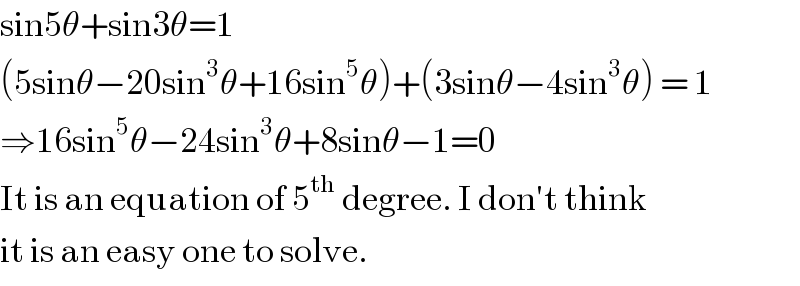
$$\mathrm{sin5}\theta+\mathrm{sin3}\theta=\mathrm{1} \\ $$$$\left(\mathrm{5sin}\theta−\mathrm{20sin}^{\mathrm{3}} \theta+\mathrm{16sin}^{\mathrm{5}} \theta\right)+\left(\mathrm{3sin}\theta−\mathrm{4sin}^{\mathrm{3}} \theta\right)\:=\:\mathrm{1} \\ $$$$\Rightarrow\mathrm{16sin}^{\mathrm{5}} \theta−\mathrm{24sin}^{\mathrm{3}} \theta+\mathrm{8sin}\theta−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{an}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{5}^{\mathrm{th}} \:\mathrm{degree}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{an}\:\mathrm{easy}\:\mathrm{one}\:\mathrm{to}\:\mathrm{solve}. \\ $$
Commented by Rio Michael last updated on 07/Jul/19
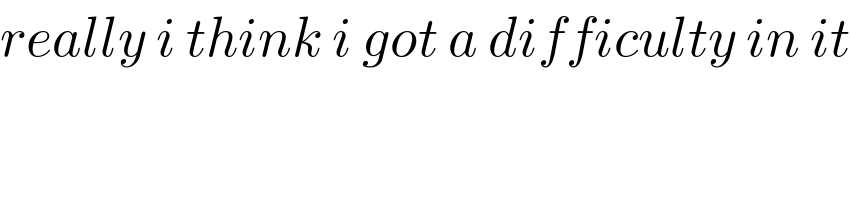
$${really}\:{i}\:{think}\:{i}\:{got}\:{a}\:{difficulty}\:{in}\:{it} \\ $$
Answered by MJS last updated on 07/Jul/19

$$\mathrm{no}\:\mathrm{exact}\:\mathrm{solution}\:\mathrm{possible} \\ $$$$\mathrm{for}\:{x}\in\left[\mathrm{0},\:\mathrm{2}\pi\left[\:\mathrm{I}\:\mathrm{get}\right.\right. \\ $$$${x}_{\mathrm{1}} \approx.\mathrm{132171549}\:\left(\approx\mathrm{7}.\mathrm{57287194}°\right) \\ $$$${x}_{\mathrm{2}} \approx.\mathrm{620008878}\:\left(\approx\mathrm{35}.\mathrm{5238919}°\right) \\ $$$${x}_{\mathrm{3}} =\pi−{x}_{\mathrm{2}} \approx\mathrm{2}.\mathrm{52158378}\:\left(\approx\mathrm{144}.\mathrm{476108}°\right) \\ $$$${x}_{\mathrm{4}} =\pi−{x}_{\mathrm{1}} \approx\mathrm{3}.\mathrm{00942110}\:\left(\approx\mathrm{172}.\mathrm{427128}°\right) \\ $$$$\Rightarrow\:\mathrm{generally}\:\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {{x}_{{i}} }}+\mathrm{2}{n}\pi\wedge{n}\in\mathbb{Z}\:\left(=\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {{x}_{{i}} }}°+{n}×\mathrm{360}°\wedge{n}\in\mathbb{Z}\right) \\ $$
Commented by Prithwish sen last updated on 08/Jul/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
