
Question Number 100899 by mhmd last updated on 29/Jun/20
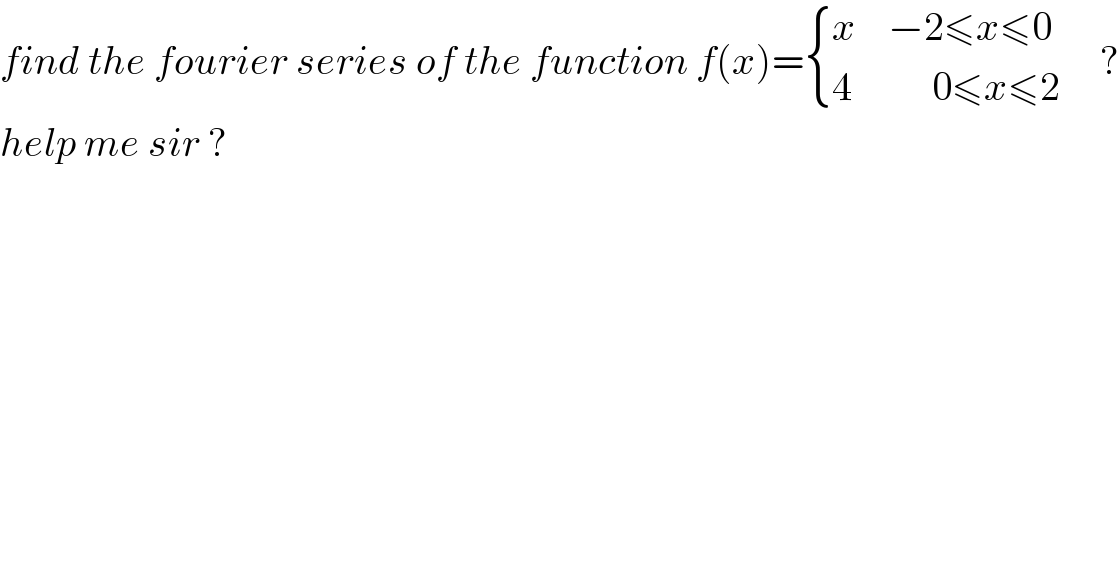
$${find}\:{the}\:{fourier}\:{series}\:{of}\:{the}\:{function}\:{f}\left({x}\right)=\begin{cases}{{x}\:\:\:\:−\mathrm{2}\leqslant{x}\leqslant\mathrm{0}\:\:\:}\\{\mathrm{4}\:\:\:\:\:\:\:\:\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{2}}\end{cases}\:\:\:? \\ $$$${help}\:{me}\:{sir}\:? \\ $$
Answered by bramlex last updated on 29/Jun/20
![f(x) : odd function. L = 4 a_n = 0 b_n = (2/L)∫_0 ^L f(x)sin (((nπx)/L)) dx b_n = (2/4)[∫_(−2) ^0 x sin (((nπx)/4))dx+∫_0 ^2 4sin (((nπx)/4)) dx] b_n =(1/2)[ ((16)/(n^2 π^2 ))sin (((nπ)/2))+(4/(nπ)) ] b_n = (8/((nπ)^2 )) sin (((nπ)/2)) + (2/(nπ)) f(x)=(a_0 /2) + Σ_(n=1) ^∞ [(8/((nπ)^2 )) sin (((nπ)/2))+(2/(nπ)) ]. cos (((nπx)/4))](Q100900.png)
$${f}\left({x}\right)\::\:{odd}\:{function}.\:{L}\:=\:\mathrm{4} \\ $$$${a}_{{n}} \:=\:\mathrm{0}\: \\ $$$${b}_{{n}} \:=\:\frac{\mathrm{2}}{{L}}\underset{\mathrm{0}} {\overset{{L}} {\int}}\:{f}\left({x}\right)\mathrm{sin}\:\left(\frac{{n}\pi{x}}{{L}}\right)\:{dx} \\ $$$${b}_{{n}} \:=\:\frac{\mathrm{2}}{\mathrm{4}}\left[\underset{−\mathrm{2}} {\overset{\mathrm{0}} {\int}}{x}\:\mathrm{sin}\:\left(\frac{{n}\pi{x}}{\mathrm{4}}\right){dx}+\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\mathrm{4sin}\:\left(\frac{{n}\pi{x}}{\mathrm{4}}\right)\:{dx}\right]\: \\ $$$${b}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{16}}{{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\mathrm{sin}\:\left(\frac{{n}\pi}{\mathrm{2}}\right)+\frac{\mathrm{4}}{{n}\pi}\:\right] \\ $$$${b}_{{n}} \:=\:\frac{\mathrm{8}}{\left({n}\pi\right)^{\mathrm{2}} }\:\mathrm{sin}\:\left(\frac{{n}\pi}{\mathrm{2}}\right)\:+\:\frac{\mathrm{2}}{{n}\pi} \\ $$$${f}\left({x}\right)=\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:+\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{8}}{\left({n}\pi\right)^{\mathrm{2}} }\:\mathrm{sin}\:\left(\frac{{n}\pi}{\mathrm{2}}\right)+\frac{\mathrm{2}}{{n}\pi}\:\right].\:\mathrm{cos}\:\left(\frac{{n}\pi{x}}{\mathrm{4}}\right)\: \\ $$
Commented by mhmd last updated on 29/Jun/20
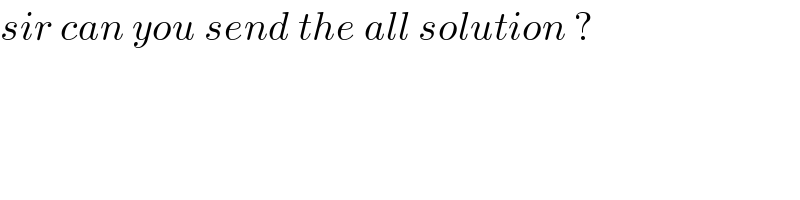
$${sir}\:{can}\:{you}\:{send}\:{the}\:{all}\:{solution}\:? \\ $$
Commented by mhmd last updated on 29/Jun/20

$${thank}\:{you}\:{sir} \\ $$
