
Question Number 169667 by MathsFan last updated on 05/May/22

$$\boldsymbol{{find}}\:\boldsymbol{{the}}\:\boldsymbol{{domain}}\:\boldsymbol{{of}} \\ $$$$\left(\boldsymbol{{i}}\right)\:\frac{\boldsymbol{{x}}}{\:\sqrt{\boldsymbol{{x}}+\mathrm{5}}} \\ $$$$\left(\boldsymbol{{ii}}\right)\:\sqrt{\boldsymbol{{x}}}+\mathrm{2} \\ $$$$\left(\boldsymbol{{iii}}\right)\:\frac{\mathrm{3}}{\:\sqrt{\boldsymbol{{x}}+\mathrm{2}}+\mathrm{5}} \\ $$
Answered by FelipeLz last updated on 06/May/22
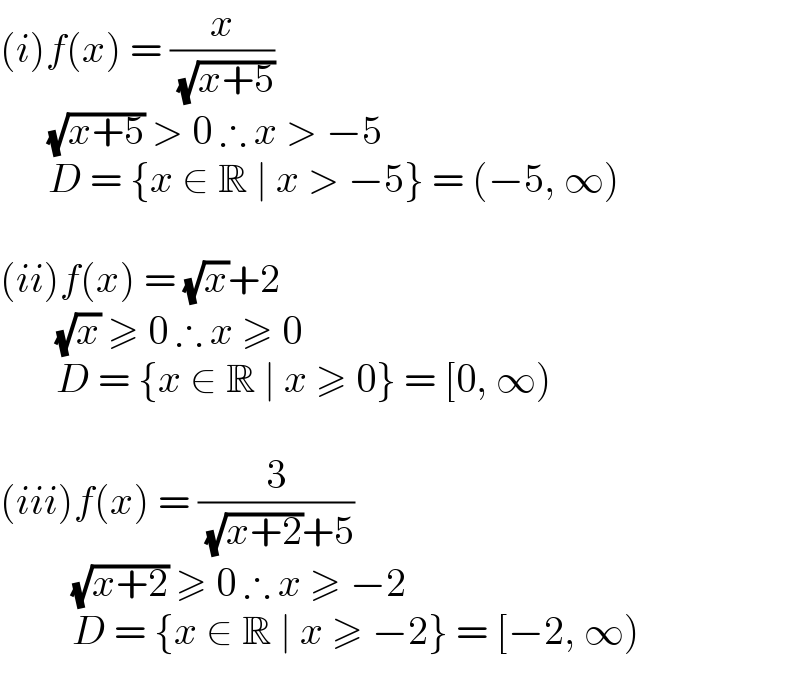
$$\left({i}\right){f}\left({x}\right)\:=\:\frac{{x}}{\:\sqrt{{x}+\mathrm{5}}} \\ $$$$\:\:\:\:\:\:\sqrt{{x}+\mathrm{5}}\:>\:\mathrm{0}\:\therefore\:{x}\:>\:−\mathrm{5} \\ $$$$\:\:\:\:\:\:{D}\:=\:\left\{{x}\:\in\:\mathbb{R}\:\mid\:{x}\:>\:−\mathrm{5}\right\}\:=\:\left(−\mathrm{5},\:\infty\right) \\ $$$$ \\ $$$$\left({ii}\right){f}\left({x}\right)\:=\:\sqrt{{x}}+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\sqrt{{x}}\:\geqslant\:\mathrm{0}\:\therefore\:{x}\:\geqslant\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{D}\:=\:\left\{{x}\:\in\:\mathbb{R}\:\mid\:{x}\:\geqslant\:\mathrm{0}\right\}\:=\:\left[\mathrm{0},\:\infty\right) \\ $$$$ \\ $$$$\left({iii}\right){f}\left({x}\right)\:=\:\frac{\mathrm{3}}{\:\sqrt{{x}+\mathrm{2}}+\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\sqrt{{x}+\mathrm{2}}\:\geqslant\:\mathrm{0}\:\therefore\:{x}\:\geqslant\:−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:{D}\:=\:\left\{{x}\:\in\:\mathbb{R}\:\mid\:{x}\:\geqslant\:−\mathrm{2}\right\}\:=\:\left[−\mathrm{2},\:\infty\right) \\ $$
Commented by MathsFan last updated on 06/May/22

$${thank}\:{you}\:{sir} \\ $$
Commented by peter frank last updated on 06/May/22

$$\mathrm{good} \\ $$
