
Question Number 113111 by gopikrishnan last updated on 11/Sep/20
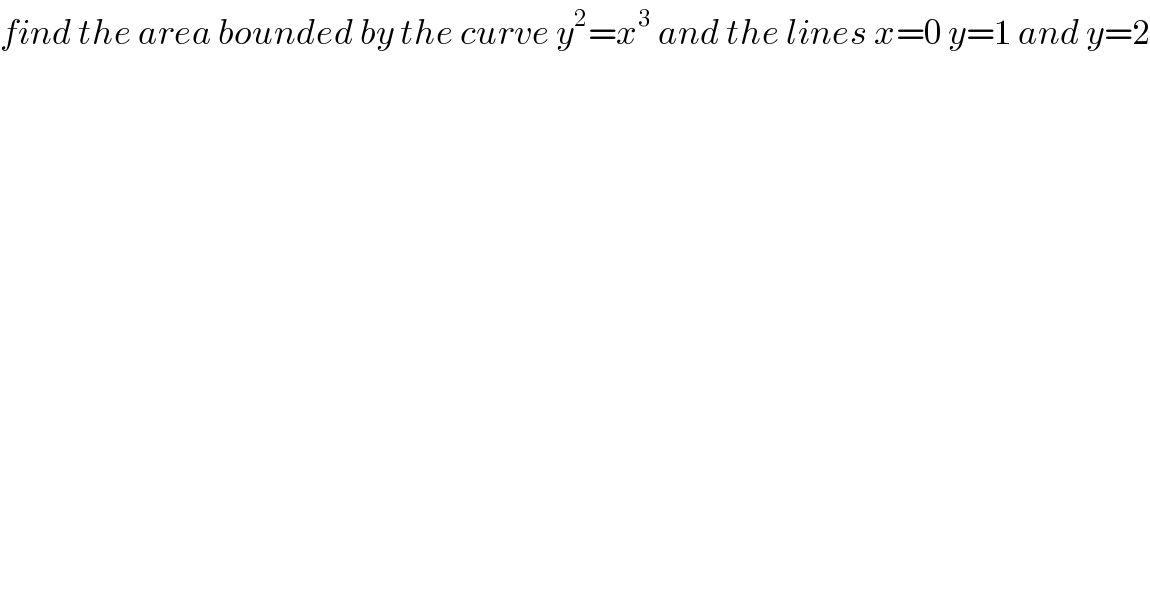
$${find}\:{the}\:{area}\:{bounded}\:{by}\:{the}\:{curve}\:{y}^{\mathrm{2}} ={x}^{\mathrm{3}} \:{and}\:{the}\:{lines}\:{x}=\mathrm{0}\:{y}=\mathrm{1}\:{and}\:{y}=\mathrm{2} \\ $$
Answered by 1549442205PVT last updated on 11/Sep/20

$$\mathrm{y}^{\mathrm{2}} =\mathrm{x}^{\mathrm{3}} \Leftrightarrow\mathrm{y}=\sqrt{\mathrm{x}^{\mathrm{3}} }\:.\mathrm{We}\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{intersection}\:\mathrm{points}\:\mathrm{of}\:\mathrm{y}=\sqrt{\mathrm{x}^{\mathrm{3}} }\:\mathrm{with} \\ $$$$\mathrm{y}=\mathrm{1}\:\mathrm{and}\:\mathrm{y}=\mathrm{2}.\mathrm{We}\:\mathrm{get} \\ $$$$\mathrm{A}\left(\mathrm{1},\mathrm{1}\right),\mathrm{B}\left(\:^{\mathrm{3}} \sqrt{\mathrm{4}},\mathrm{2}\right).\mathrm{Hence}, \\ $$$$\mathrm{S}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{2}−\mathrm{1}\right)\mathrm{dx}+\int_{\mathrm{1}} ^{\:\:^{\mathrm{3}} \sqrt{\mathrm{4}}} \left(\mathrm{2}−\sqrt{\mathrm{x}^{\mathrm{3}} \:}\:\right)\mathrm{dx} \\ $$$$=\mathrm{x}\mid_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{2x}\mid_{\mathrm{1}} ^{\:^{\mathrm{3}} \sqrt{\mathrm{4}}} −\frac{\mathrm{2}}{\mathrm{5}}\mathrm{x}^{\frac{\mathrm{5}}{\mathrm{2}}} \mid_{\mathrm{1}} ^{\:^{\mathrm{3}} \sqrt{\mathrm{4}}} = \\ $$$$=\mathrm{1}+\mathrm{2}\left(\:^{\mathrm{3}} \sqrt{\mathrm{4}}\:−\mathrm{1}\right)−\frac{\mathrm{2}}{\mathrm{5}}\left(\:^{\mathrm{6}} \sqrt{\mathrm{4}^{\mathrm{5}} }\:−\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{3}}{\mathrm{5}}+\mathrm{2}\:^{\mathrm{3}} \sqrt{\mathrm{4}}\:−\frac{\mathrm{2}}{\mathrm{5}}\:^{\mathrm{6}} \sqrt{\mathrm{4}^{\mathrm{5}} }\:\approx\mathrm{1}.\mathrm{304881262} \\ $$
Commented by gopikrishnan last updated on 11/Sep/20

$${Thank}\:{u}\:{sir} \\ $$
Commented by 1549442205PVT last updated on 12/Sep/20
$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}. \\ $$
