
Question Number 80027 by jagoll last updated on 30/Jan/20
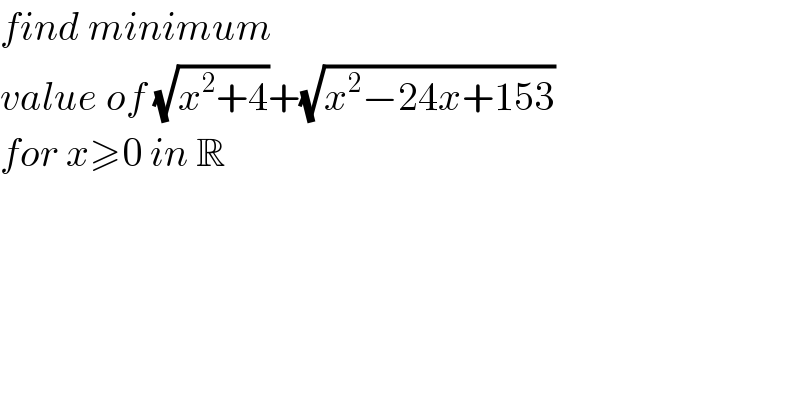
$${find}\:{minimum} \\ $$$${value}\:{of}\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}+\sqrt{{x}^{\mathrm{2}} −\mathrm{24}{x}+\mathrm{153}} \\ $$$${for}\:{x}\geqslant\mathrm{0}\:{in}\:\mathbb{R} \\ $$
Commented by john santu last updated on 30/Jan/20

$$\mathrm{yes}\:\mathrm{sir} \\ $$
Commented by john santu last updated on 30/Jan/20

$$\mathrm{f}'\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}}+\frac{\mathrm{x}−\mathrm{12}}{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{24x}+\mathrm{153}}}\:=\mathrm{0} \\ $$$$\frac{\mathrm{x}}{\mathrm{12}−\mathrm{x}}\:=\sqrt{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}{\mathrm{x}^{\mathrm{2}} −\mathrm{24x}+\mathrm{153}}} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{144}−\mathrm{24x}+\mathrm{x}^{\mathrm{2}} }\:=\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{24x}+\mathrm{153}} \\ $$$$\mathrm{x}^{\mathrm{4}} −\mathrm{24x}^{\mathrm{3}} +\mathrm{153x}^{\mathrm{2}} =\mathrm{x}^{\mathrm{4}} −\mathrm{24x}^{\mathrm{3}} +\mathrm{144x}^{\mathrm{2}} \\ $$$$+\mathrm{4x}^{\mathrm{2}} −\mathrm{96x}+\mathrm{576} \\ $$$$\mathrm{5x}^{\mathrm{2}} +\mathrm{96x}−\mathrm{576}=\mathrm{0} \\ $$$$\mathrm{x}\:=\frac{−\mathrm{96}+\sqrt{\mathrm{20736}}}{\mathrm{10}}\:=\:\frac{−\mathrm{96}+\mathrm{144}}{\mathrm{10}}=\mathrm{4}.\mathrm{8} \\ $$$$\mathrm{f}_{\mathrm{min}} =\:\sqrt{\left(\frac{\mathrm{24}}{\mathrm{5}}\right)^{\mathrm{2}} +\mathrm{4}}+\sqrt{\left(\frac{\mathrm{24}}{\mathrm{5}}−\mathrm{12}\right)^{\mathrm{2}} +\mathrm{9}} \\ $$$$\:\:\:\:\:\:\: \\ $$
Commented by mr W last updated on 30/Jan/20
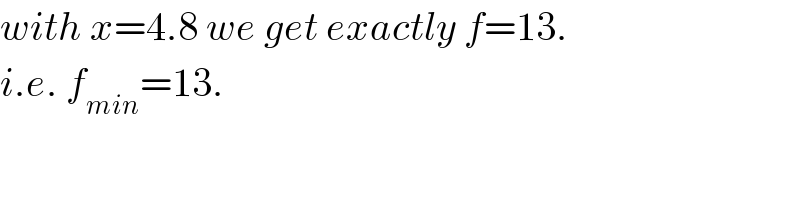
$${with}\:{x}=\mathrm{4}.\mathrm{8}\:{we}\:{get}\:{exactly}\:{f}=\mathrm{13}. \\ $$$${i}.{e}.\:{f}_{{min}} =\mathrm{13}. \\ $$
Commented by jagoll last updated on 30/Jan/20
$${thanks}\:{mr}\:{w}\:{and}\:{john} \\ $$
