Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 197752 by cortano12 last updated on 27/Sep/23

find minimum value of m such that m^(19) = 1800 (mod 2029)

$$\:\mathrm{find}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{m} \\ $$$$\:\mathrm{such}\:\mathrm{that}\:\mathrm{m}^{\mathrm{19}} =\:\mathrm{1800}\:\left(\mathrm{mod}\:\mathrm{2029}\right) \\ $$

Answered by deleteduser1 last updated on 27/Sep/23

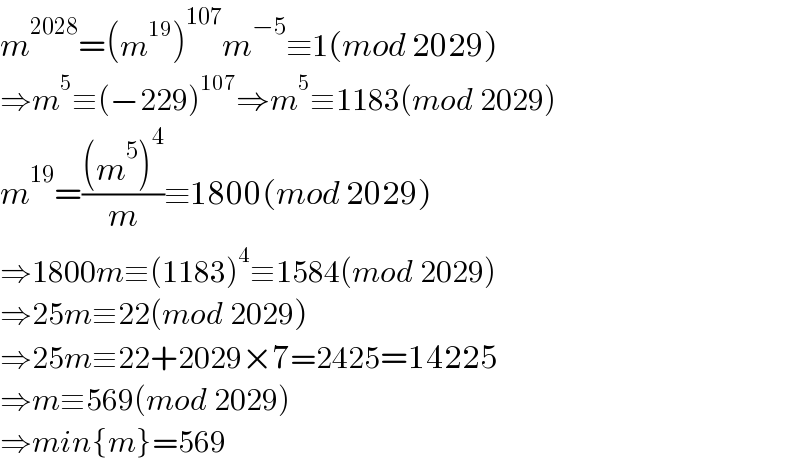
m^(2028) =(m^(19) )^(107) m^(−5) ≡1(mod 2029) ⇒m^5 ≡(−229)^(107) ⇒m^5 ≡1183(mod 2029) m^(19) =(((m^5 )^4 )/m)≡1800(mod 2029) ⇒1800m≡(1183)^4 ≡1584(mod 2029) ⇒25m≡22(mod 2029) ⇒25m≡22+2029×7=2425=14225 ⇒m≡569(mod 2029) ⇒min{m}=569

$${m}^{\mathrm{2028}} =\left({m}^{\mathrm{19}} \right)^{\mathrm{107}} {m}^{−\mathrm{5}} \equiv\mathrm{1}\left({mod}\:\mathrm{2029}\right) \\ $$$$\Rightarrow{m}^{\mathrm{5}} \equiv\left(−\mathrm{229}\right)^{\mathrm{107}} \Rightarrow{m}^{\mathrm{5}} \equiv\mathrm{1183}\left({mod}\:\mathrm{2029}\right) \\ $$$${m}^{\mathrm{19}} =\frac{\left({m}^{\mathrm{5}} \right)^{\mathrm{4}} }{{m}}\equiv\mathrm{1800}\left({mod}\:\mathrm{2029}\right) \\ $$$$\Rightarrow\mathrm{1800}{m}\equiv\left(\mathrm{1183}\right)^{\mathrm{4}} \equiv\mathrm{1584}\left({mod}\:\mathrm{2029}\right) \\ $$$$\Rightarrow\mathrm{25}{m}\equiv\mathrm{22}\left({mod}\:\mathrm{2029}\right) \\ $$$$\Rightarrow\mathrm{25}{m}\equiv\mathrm{22}+\mathrm{2029}×\mathrm{7}=\mathrm{2425}=\mathrm{14225} \\ $$$$\Rightarrow{m}\equiv\mathrm{569}\left({mod}\:\mathrm{2029}\right) \\ $$$$\Rightarrow{min}\left\{{m}\right\}=\mathrm{569} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com