
Question Number 104533 by 175mohamed last updated on 22/Jul/20
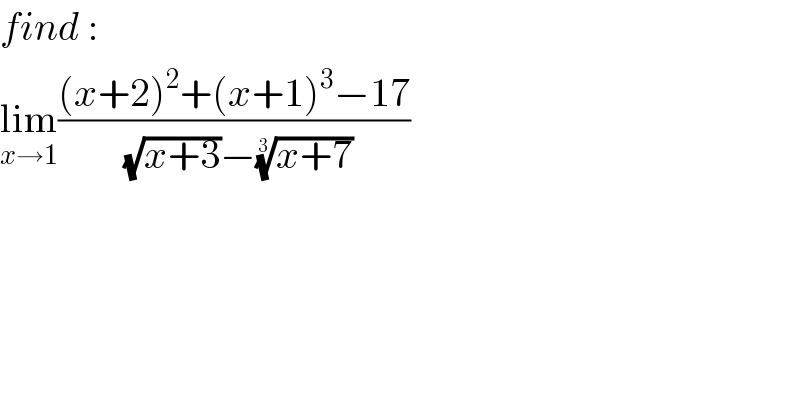
$${find}\:: \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\left({x}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{17}}{\sqrt{{x}+\mathrm{3}}−\sqrt[{\mathrm{3}}]{{x}+\mathrm{7}}} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Jul/20
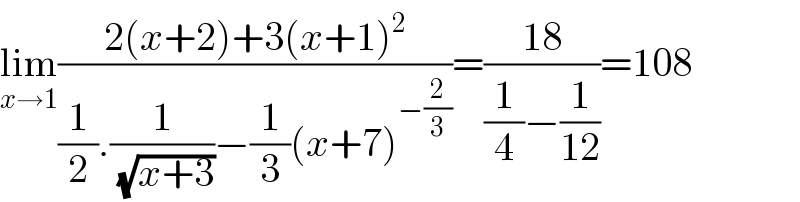
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}\left({x}+\mathrm{2}\right)+\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\sqrt{{x}+\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{3}}\left({x}+\mathrm{7}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} }=\frac{\mathrm{18}}{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{12}}}=\mathrm{108} \\ $$
Answered by OlafThorendsen last updated on 22/Jul/20
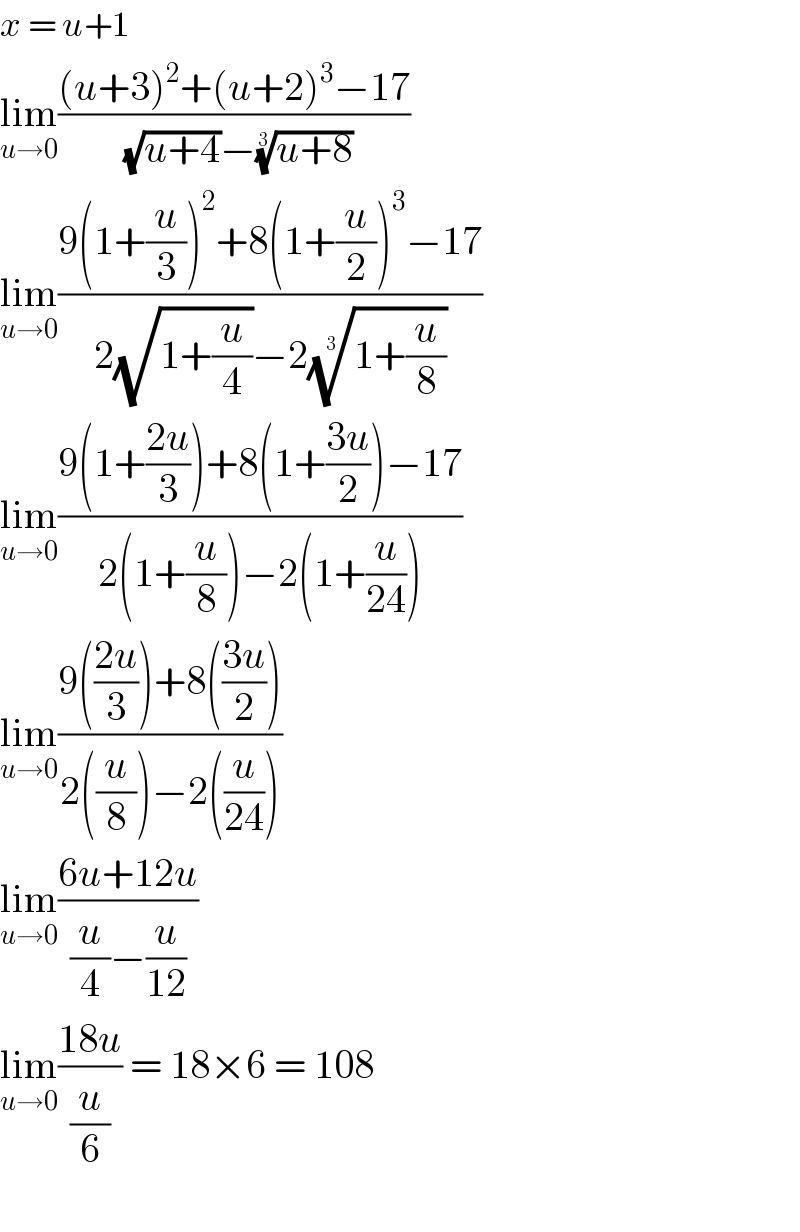
$${x}\:=\:{u}+\mathrm{1} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({u}+\mathrm{3}\right)^{\mathrm{2}} +\left({u}+\mathrm{2}\right)^{\mathrm{3}} −\mathrm{17}}{\sqrt{{u}+\mathrm{4}}−\sqrt[{\mathrm{3}}]{{u}+\mathrm{8}}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{9}\left(\mathrm{1}+\frac{{u}}{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{8}\left(\mathrm{1}+\frac{{u}}{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{17}}{\mathrm{2}\sqrt{\mathrm{1}+\frac{{u}}{\mathrm{4}}}−\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{{u}}{\mathrm{8}}}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{9}\left(\mathrm{1}+\frac{\mathrm{2}{u}}{\mathrm{3}}\right)+\mathrm{8}\left(\mathrm{1}+\frac{\mathrm{3}{u}}{\mathrm{2}}\right)−\mathrm{17}}{\mathrm{2}\left(\mathrm{1}+\frac{{u}}{\mathrm{8}}\right)−\mathrm{2}\left(\mathrm{1}+\frac{{u}}{\mathrm{24}}\right)} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{9}\left(\frac{\mathrm{2}{u}}{\mathrm{3}}\right)+\mathrm{8}\left(\frac{\mathrm{3}{u}}{\mathrm{2}}\right)}{\mathrm{2}\left(\frac{{u}}{\mathrm{8}}\right)−\mathrm{2}\left(\frac{{u}}{\mathrm{24}}\right)} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{6}{u}+\mathrm{12}{u}}{\frac{{u}}{\mathrm{4}}−\frac{{u}}{\mathrm{12}}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{18}{u}}{\frac{{u}}{\mathrm{6}}}\:=\:\mathrm{18}×\mathrm{6}\:=\:\mathrm{108} \\ $$$$ \\ $$
Commented by bobhans last updated on 22/Jul/20
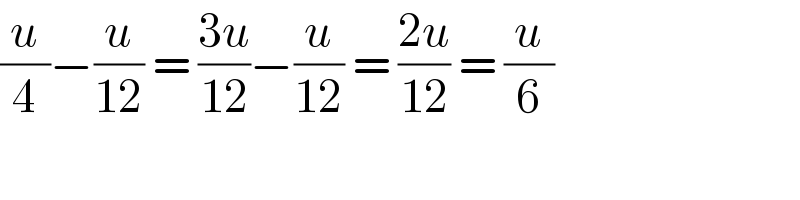
$$\frac{{u}}{\mathrm{4}}−\frac{{u}}{\mathrm{12}}\:=\:\frac{\mathrm{3}{u}}{\mathrm{12}}−\frac{{u}}{\mathrm{12}}\:=\:\frac{\mathrm{2}{u}}{\mathrm{12}}\:=\:\frac{{u}}{\mathrm{6}} \\ $$
Answered by bramlex last updated on 22/Jul/20
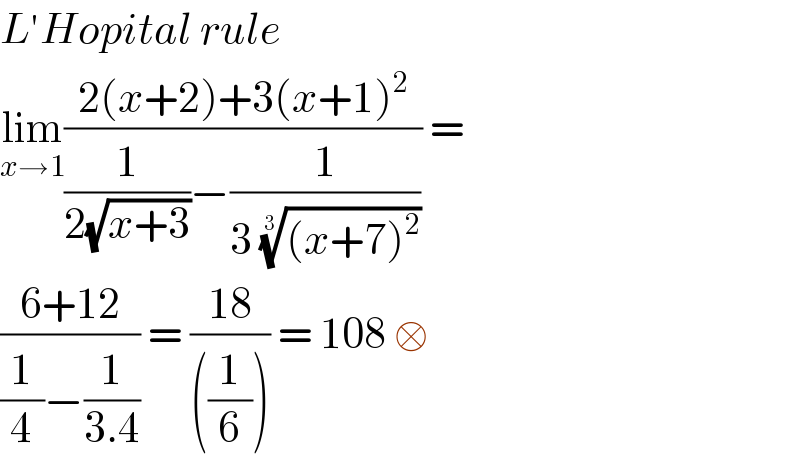
$${L}'{Hopital}\:{rule}\: \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}\left({x}+\mathrm{2}\right)+\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{3}\:\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{7}\right)^{\mathrm{2}} }}}\:= \\ $$$$\frac{\mathrm{6}+\mathrm{12}}{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{4}}}\:=\:\frac{\mathrm{18}}{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)}\:=\:\mathrm{108}\:\square \\ $$
