
Question Number 48177 by Abdo msup. last updated on 20/Nov/18
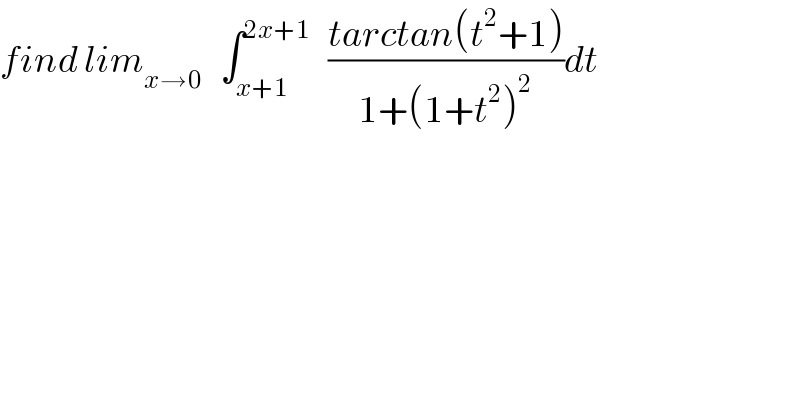
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\int_{{x}+\mathrm{1}} ^{\mathrm{2}{x}+\mathrm{1}} \:\:\:\frac{{tarctan}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{1}+\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$
Commented by kaivan.ahmadi last updated on 21/Nov/18

$$\mathrm{it}\:\mathrm{is}\:\mathrm{zero} \\ $$
Commented by Abdo msup. last updated on 21/Nov/18
![let A(x)=∫_(x+1) ^(2x+1) (t/(1+(1+t^2 )^2 )) arctan(t^2 +1)dt by parts u^′ =(t/(1+(1+t^2 )^2 )) and v=arctan(t^2 +1)⇒ A(x)=[(1/2)arctan(1+t^2 ).arctan(1+t^2 )]_(x+1) ^(2x+1) −∫_(x+1) ^(2x+1) (1/2)arctan(1+t^2 ) ((2t)/(1+(1+t^2 )^2 ))dt =(1/2)( arctan^2 (1+(2x+1)^2 )−arctan(1+(x+1)^2 )) −A(x) ⇒ A(x)=(1/4){ arctan^2 (1+(2x+1)^2 )−arctan(1+(x+1)^2 )}⇒ lim_(x→0) A(x)=(1/4){arctan^2 (2)−arctan^2 (2)} =0.](Q48253.png)
$${let}\:{A}\left({x}\right)=\int_{{x}+\mathrm{1}} ^{\mathrm{2}{x}+\mathrm{1}} \:\:\frac{{t}}{\mathrm{1}+\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{arctan}\left({t}^{\mathrm{2}} +\mathrm{1}\right){dt}\:{by}\:{parts} \\ $$$${u}^{'} =\frac{{t}}{\mathrm{1}+\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{and}\:{v}={arctan}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\Rightarrow \\ $$$${A}\left({x}\right)=\left[\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\mathrm{1}+{t}^{\mathrm{2}} \right).{arctan}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right]_{{x}+\mathrm{1}} ^{\mathrm{2}{x}+\mathrm{1}} \\ $$$$−\int_{{x}+\mathrm{1}} ^{\mathrm{2}{x}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:\frac{\mathrm{2}{t}}{\mathrm{1}+\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\:{arctan}^{\mathrm{2}} \left(\mathrm{1}+\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \right)−{arctan}\left(\mathrm{1}+\left({x}+\mathrm{1}\right)^{\mathrm{2}} \right)\right) \\ $$$$−{A}\left({x}\right)\:\Rightarrow \\ $$$${A}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:{arctan}^{\mathrm{2}} \left(\mathrm{1}+\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \right)−{arctan}\left(\mathrm{1}+\left({x}+\mathrm{1}\right)^{\mathrm{2}} \right)\right\}\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {A}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left\{{arctan}^{\mathrm{2}} \left(\mathrm{2}\right)−{arctan}^{\mathrm{2}} \left(\mathrm{2}\right)\right\}\:=\mathrm{0}. \\ $$
