Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 212926 by efronzo1 last updated on 27/Oct/24

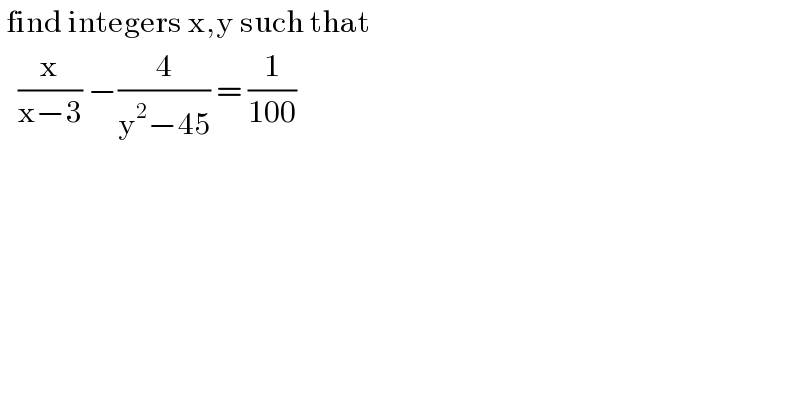
find integers x,y such that (x/(x−3)) −(4/(y^2 −45)) = (1/(100))

$$\:\mathrm{find}\:\mathrm{integers}\:\mathrm{x},\mathrm{y}\:\mathrm{such}\:\mathrm{that}\: \\ $$$$\:\:\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{3}}\:−\frac{\mathrm{4}}{\mathrm{y}^{\mathrm{2}} −\mathrm{45}}\:=\:\frac{\mathrm{1}}{\mathrm{100}} \\ $$

Answered by Frix last updated on 27/Oct/24

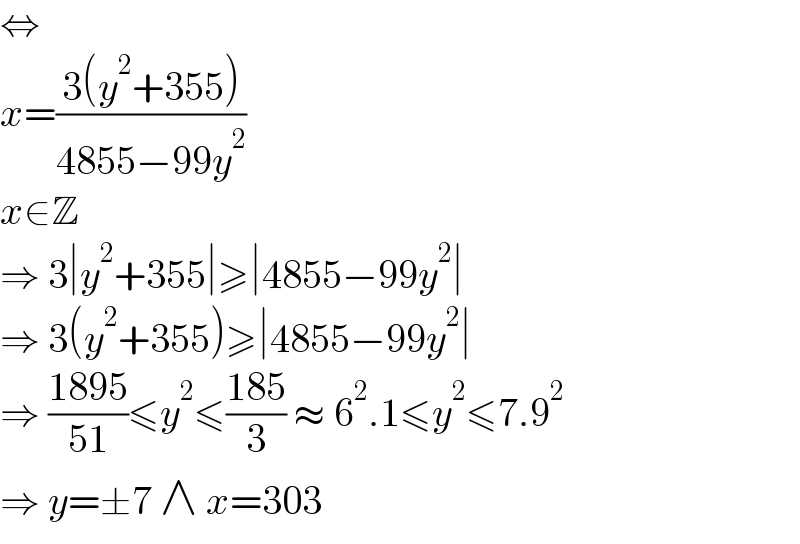
⇔ x=((3(y^2 +355))/(4855−99y^2 )) x∈Z ⇒ 3∣y^2 +355∣≥∣4855−99y^2 ∣ ⇒ 3(y^2 +355)≥∣4855−99y^2 ∣ ⇒ ((1895)/(51))≤y^2 ≤((185)/3) ≈ 6^2 .1≤y^2 ≤7.9^2 ⇒ y=±7 ∧ x=303

$$\Leftrightarrow \\ $$$${x}=\frac{\mathrm{3}\left({y}^{\mathrm{2}} +\mathrm{355}\right)}{\mathrm{4855}−\mathrm{99}{y}^{\mathrm{2}} } \\ $$$${x}\in\mathbb{Z} \\ $$$$\Rightarrow\:\mathrm{3}\mid{y}^{\mathrm{2}} +\mathrm{355}\mid\geqslant\mid\mathrm{4855}−\mathrm{99}{y}^{\mathrm{2}} \mid \\ $$$$\Rightarrow\:\mathrm{3}\left({y}^{\mathrm{2}} +\mathrm{355}\right)\geqslant\mid\mathrm{4855}−\mathrm{99}{y}^{\mathrm{2}} \mid \\ $$$$\Rightarrow\:\frac{\mathrm{1895}}{\mathrm{51}}\leqslant{y}^{\mathrm{2}} \leqslant\frac{\mathrm{185}}{\mathrm{3}}\:\approx\:\mathrm{6}^{\mathrm{2}} .\mathrm{1}\leqslant{y}^{\mathrm{2}} \leqslant\mathrm{7}.\mathrm{9}^{\mathrm{2}} \\ $$$$\Rightarrow\:{y}=\pm\mathrm{7}\:\wedge\:{x}=\mathrm{303} \\ $$

Answered by Rasheed.Sindhi last updated on 28/Oct/24

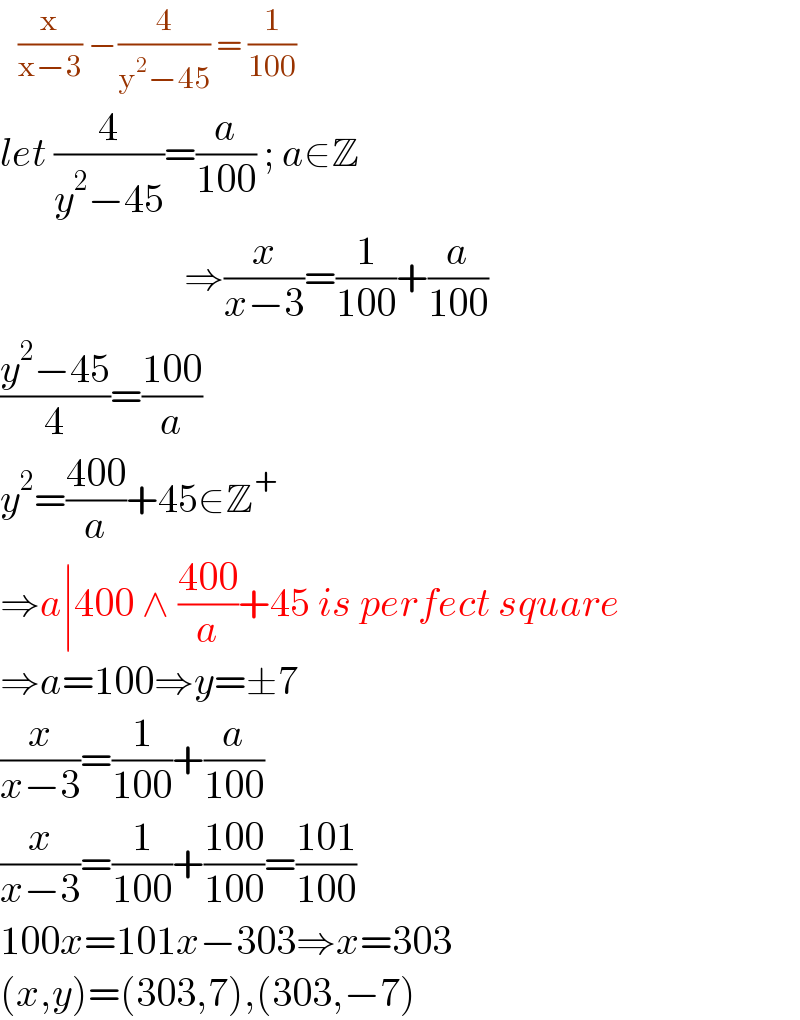
(x/(x−3)) −(4/(y^2 −45)) = (1/(100)) let (4/(y^2 −45))=(a/(100)) ; a∈Z ⇒(x/(x−3))=(1/(100))+(a/(100)) ((y^2 −45)/4)=((100)/a) y^2 =((400)/a)+45∈Z^+ ⇒a∣400 ∧ ((400)/a)+45 is perfect square ⇒a=100⇒y=±7 (x/(x−3))=(1/(100))+(a/(100)) (x/(x−3))=(1/(100))+((100)/(100))=((101)/(100)) 100x=101x−303⇒x=303 (x,y)=(303,7),(303,−7)

$$\:\:\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{3}}\:−\frac{\mathrm{4}}{\mathrm{y}^{\mathrm{2}} −\mathrm{45}}\:=\:\frac{\mathrm{1}}{\mathrm{100}} \\ $$$${let}\:\frac{\mathrm{4}}{{y}^{\mathrm{2}} −\mathrm{45}}=\frac{{a}}{\mathrm{100}}\:;\:{a}\in\mathbb{Z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\frac{{x}}{{x}−\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{100}}+\frac{{a}}{\mathrm{100}} \\ $$$$\frac{{y}^{\mathrm{2}} −\mathrm{45}}{\mathrm{4}}=\frac{\mathrm{100}}{{a}} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{400}}{{a}}+\mathrm{45}\in\mathbb{Z}^{+} \\ $$$$\Rightarrow{a}\mid\mathrm{400}\:\wedge\:\frac{\mathrm{400}}{{a}}+\mathrm{45}\:{is}\:{perfect}\:{square} \\ $$$$\Rightarrow{a}=\mathrm{100}\Rightarrow{y}=\pm\mathrm{7} \\ $$$$\frac{{x}}{{x}−\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{100}}+\frac{{a}}{\mathrm{100}} \\ $$$$\frac{{x}}{{x}−\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{100}}+\frac{\mathrm{100}}{\mathrm{100}}=\frac{\mathrm{101}}{\mathrm{100}} \\ $$$$\mathrm{100}{x}=\mathrm{101}{x}−\mathrm{303}\Rightarrow{x}=\mathrm{303} \\ $$$$\left({x},{y}\right)=\left(\mathrm{303},\mathrm{7}\right),\left(\mathrm{303},−\mathrm{7}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com