
Question Number 84624 by subhankar10 last updated on 14/Mar/20
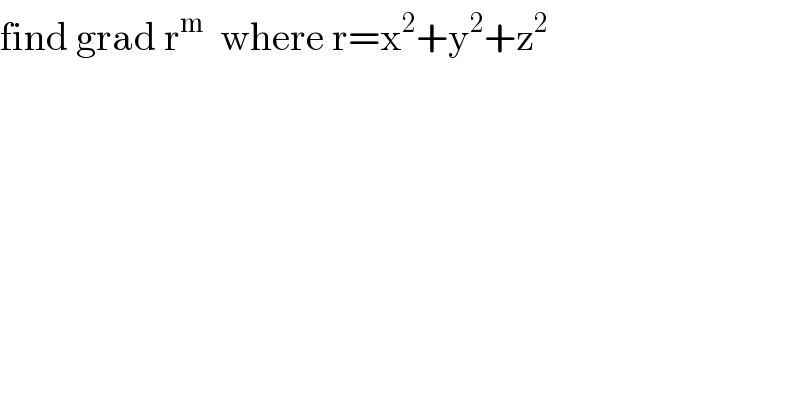
$$\mathrm{find}\:\mathrm{grad}\:\mathrm{r}^{\mathrm{m}} \:\:\mathrm{where}\:\mathrm{r}=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \\ $$
Answered by TANMAY PANACEA last updated on 14/Mar/20
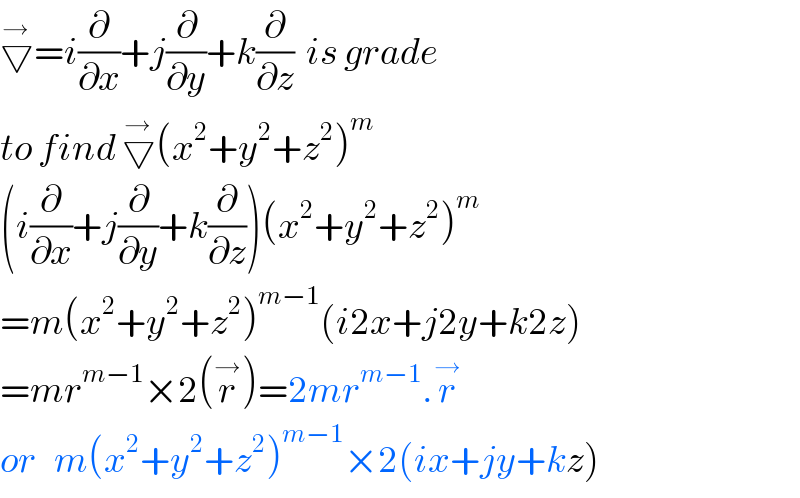
$$\overset{\rightarrow} {\bigtriangledown}={i}\frac{\partial}{\partial{x}}+{j}\frac{\partial}{\partial{y}}+{k}\frac{\partial}{\partial{z}}\:\:{is}\:{grade} \\ $$$${to}\:{find}\:\overset{\rightarrow} {\bigtriangledown}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{{m}} \\ $$$$\left({i}\frac{\partial}{\partial{x}}+{j}\frac{\partial}{\partial{y}}+{k}\frac{\partial}{\partial{z}}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{{m}} \\ $$$$={m}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{{m}−\mathrm{1}} \left({i}\mathrm{2}{x}+{j}\mathrm{2}{y}+{k}\mathrm{2}{z}\right) \\ $$$$={mr}^{{m}−\mathrm{1}} ×\mathrm{2}\left(\overset{\rightarrow} {{r}}\right)=\mathrm{2}{mr}^{{m}−\mathrm{1}} .\overset{\rightarrow} {{r}} \\ $$$${or}\:\:\:{m}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{{m}−\mathrm{1}} ×\mathrm{2}\left({ix}+{jy}+{kz}\right) \\ $$
Commented by subhankar10 last updated on 15/Mar/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TANMAY PANACEA last updated on 15/Mar/20

$${most}\:{welcome} \\ $$
