
Question Number 69764 by Rio Michael last updated on 27/Sep/19
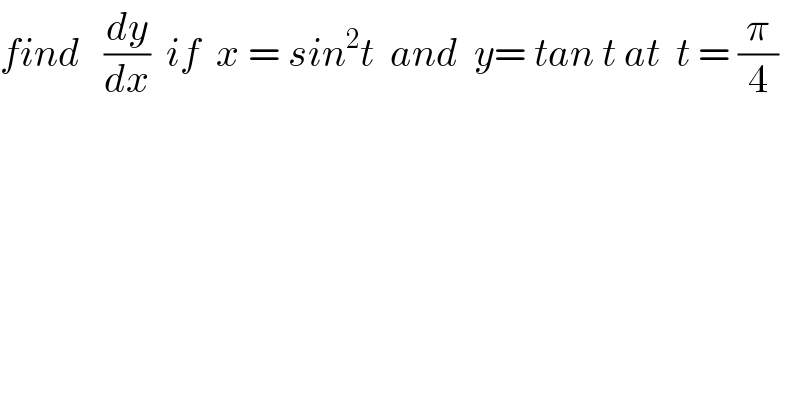
$${find}\:\:\:\frac{{dy}}{{dx}}\:\:{if}\:\:{x}\:=\:{sin}^{\mathrm{2}} {t}\:\:{and}\:\:{y}=\:{tan}\:{t}\:{at}\:\:{t}\:=\:\frac{\pi}{\mathrm{4}} \\ $$
Commented by kaivan.ahmadi last updated on 27/Sep/19

$$\frac{{dy}}{{dx}}=\frac{\frac{{dy}}{{dt}}}{\frac{{dx}}{{dt}}}=\frac{\mathrm{1}+{tan}^{\mathrm{2}} {t}}{{sin}\mathrm{2}{t}} \\ $$
Answered by mind is power last updated on 27/Sep/19
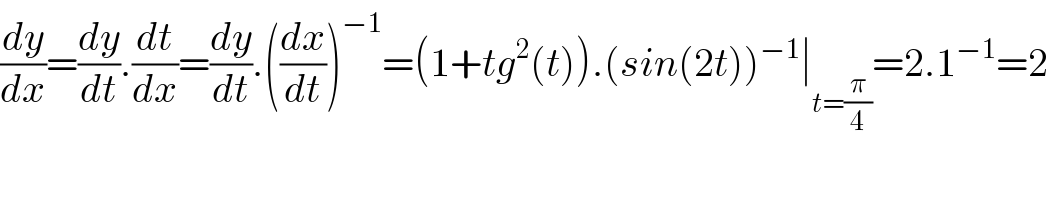
$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}.\frac{{dt}}{{dx}}=\frac{{dy}}{{dt}}.\left(\frac{{dx}}{{dt}}\right)^{−\mathrm{1}} =\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right).\left({sin}\left(\mathrm{2}{t}\right)\right)^{−\mathrm{1}} \mid_{{t}=\frac{\pi}{\mathrm{4}}} =\mathrm{2}.\mathrm{1}^{−\mathrm{1}} =\mathrm{2} \\ $$$$ \\ $$
