Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 120912 by bemath last updated on 04/Nov/20

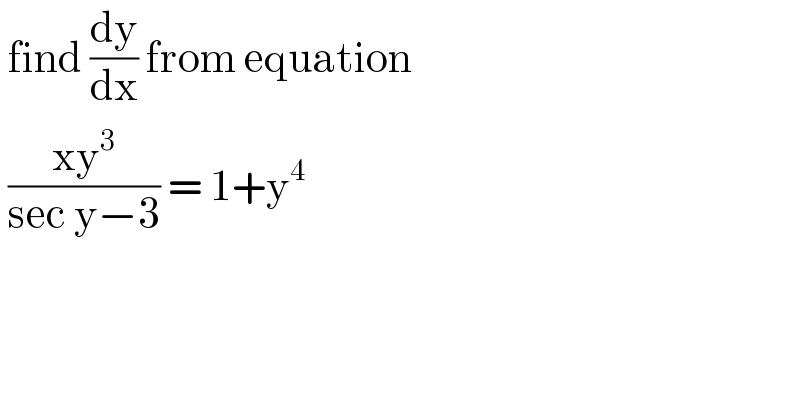
find (dy/dx) from equation ((xy^3 )/(sec y−3)) = 1+y^4

$$\:\mathrm{find}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\mathrm{from}\:\mathrm{equation}\: \\ $$$$\:\frac{\mathrm{xy}^{\mathrm{3}} }{\mathrm{sec}\:\mathrm{y}−\mathrm{3}}\:=\:\mathrm{1}+\mathrm{y}^{\mathrm{4}} \\ $$

Answered by liberty last updated on 04/Nov/20

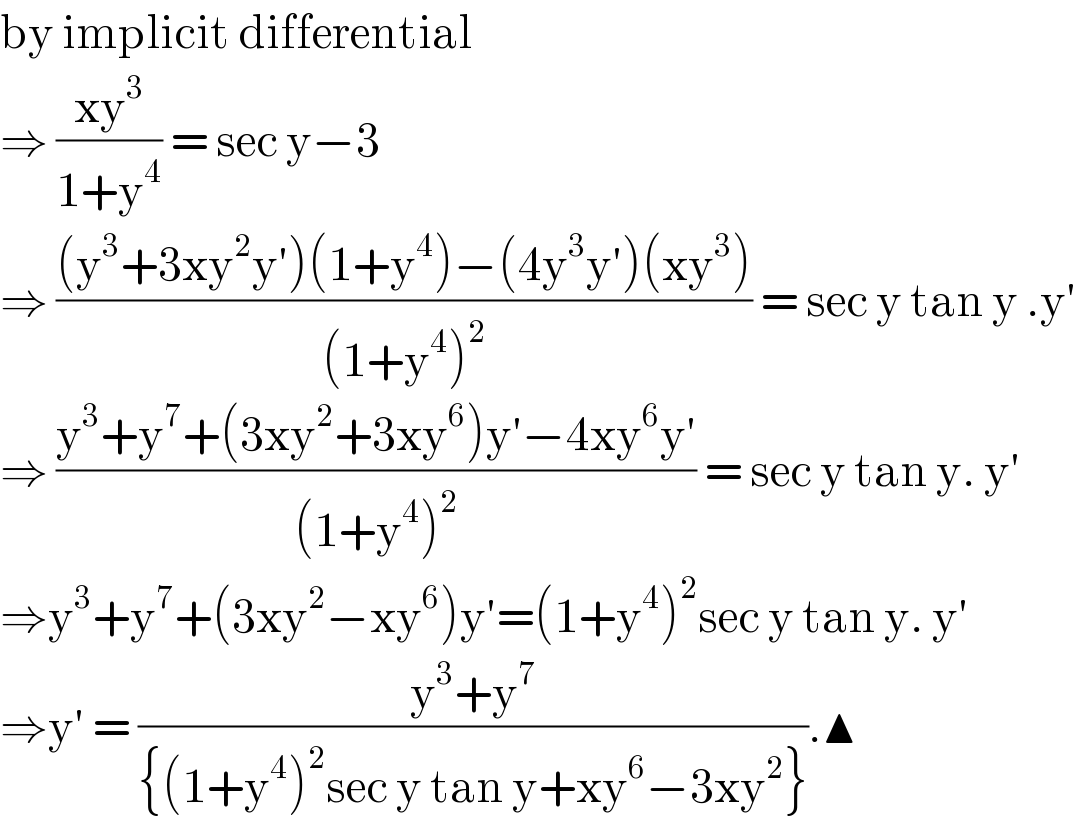
by implicit differential ⇒ ((xy^3 )/(1+y^4 )) = sec y−3 ⇒ (((y^3 +3xy^2 y′)(1+y^4 )−(4y^3 y′)(xy^3 ))/((1+y^4 )^2 )) = sec y tan y .y′ ⇒ ((y^3 +y^7 +(3xy^2 +3xy^6 )y′−4xy^6 y′)/((1+y^4 )^2 )) = sec y tan y. y′ ⇒y^3 +y^7 +(3xy^2 −xy^6 )y′=(1+y^4 )^2 sec y tan y. y′ ⇒y′ = ((y^3 +y^7 )/({(1+y^4 )^2 sec y tan y+xy^6 −3xy^2 })).▲

$$\mathrm{by}\:\mathrm{implicit}\:\mathrm{differential}\: \\ $$$$\Rightarrow\:\frac{\mathrm{xy}^{\mathrm{3}} }{\mathrm{1}+\mathrm{y}^{\mathrm{4}} }\:=\:\mathrm{sec}\:\mathrm{y}−\mathrm{3} \\ $$$$\Rightarrow\:\frac{\left(\mathrm{y}^{\mathrm{3}} +\mathrm{3xy}^{\mathrm{2}} \mathrm{y}'\right)\left(\mathrm{1}+\mathrm{y}^{\mathrm{4}} \right)−\left(\mathrm{4y}^{\mathrm{3}} \mathrm{y}'\right)\left(\mathrm{xy}^{\mathrm{3}} \right)}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{4}} \right)^{\mathrm{2}} }\:=\:\mathrm{sec}\:\mathrm{y}\:\mathrm{tan}\:\mathrm{y}\:.\mathrm{y}' \\ $$$$\Rightarrow\:\frac{\mathrm{y}^{\mathrm{3}} +\mathrm{y}^{\mathrm{7}} +\left(\mathrm{3xy}^{\mathrm{2}} +\mathrm{3xy}^{\mathrm{6}} \right)\mathrm{y}'−\mathrm{4xy}^{\mathrm{6}} \mathrm{y}'}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{4}} \right)^{\mathrm{2}} }\:=\:\mathrm{sec}\:\mathrm{y}\:\mathrm{tan}\:\mathrm{y}.\:\mathrm{y}' \\ $$$$\Rightarrow\mathrm{y}^{\mathrm{3}} +\mathrm{y}^{\mathrm{7}} +\left(\mathrm{3xy}^{\mathrm{2}} −\mathrm{xy}^{\mathrm{6}} \right)\mathrm{y}'=\left(\mathrm{1}+\mathrm{y}^{\mathrm{4}} \right)^{\mathrm{2}} \mathrm{sec}\:\mathrm{y}\:\mathrm{tan}\:\mathrm{y}.\:\mathrm{y}' \\ $$$$\Rightarrow\mathrm{y}'\:=\:\frac{\mathrm{y}^{\mathrm{3}} +\mathrm{y}^{\mathrm{7}} }{\left\{\left(\mathrm{1}+\mathrm{y}^{\mathrm{4}} \right)^{\mathrm{2}} \mathrm{sec}\:\mathrm{y}\:\mathrm{tan}\:\mathrm{y}+\mathrm{xy}^{\mathrm{6}} −\mathrm{3xy}^{\mathrm{2}} \right\}}.\blacktriangle \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com