
Question Number 31055 by abdo imad last updated on 02/Mar/18
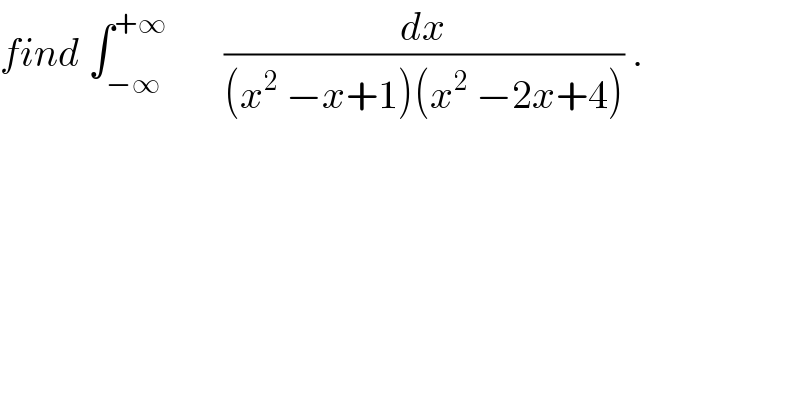
$${find}\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:−{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:−\mathrm{2}{x}+\mathrm{4}\right)}\:. \\ $$
Commented by abdo imad last updated on 03/Mar/18
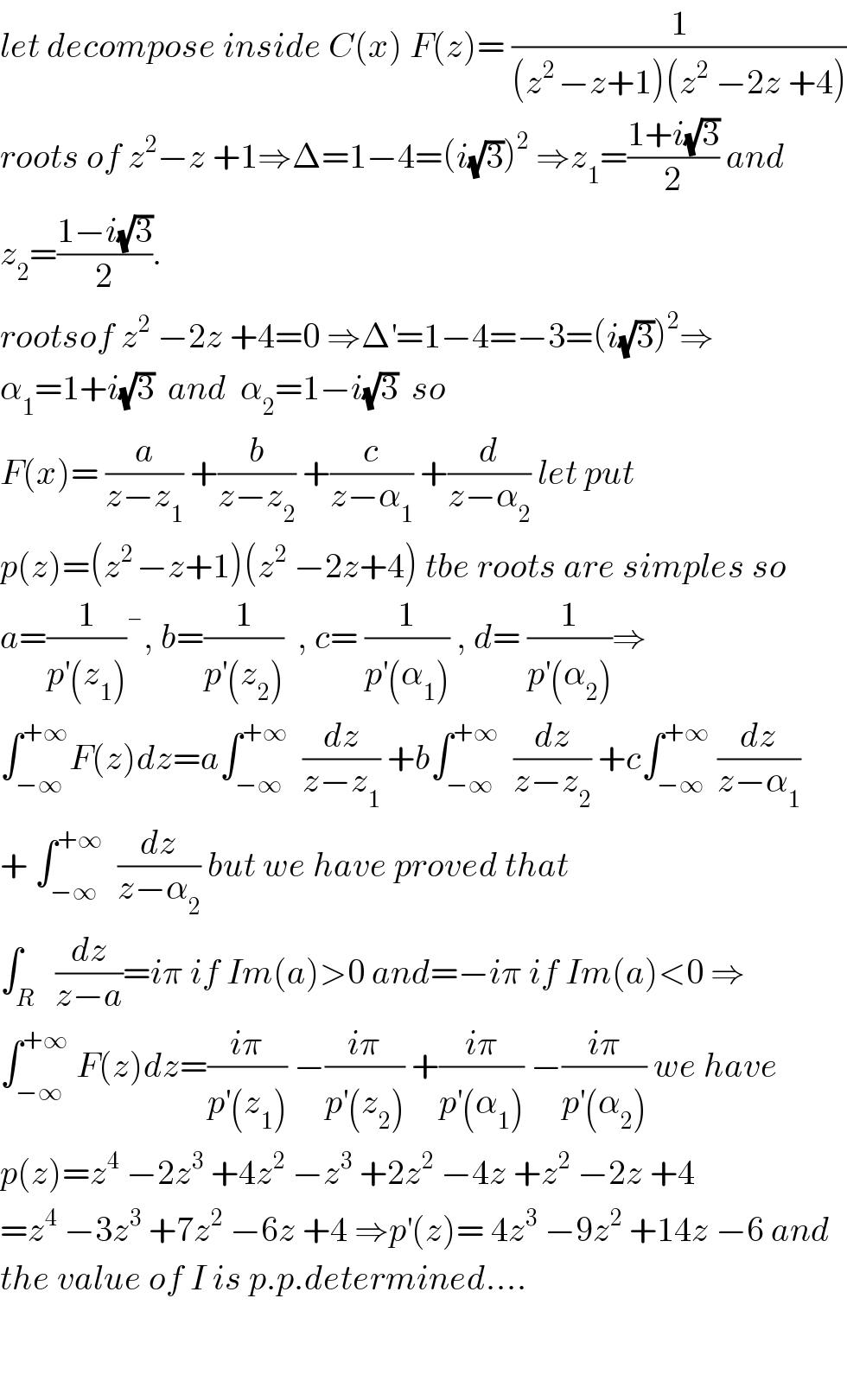
$${let}\:{decompose}\:{inside}\:{C}\left({x}\right)\:{F}\left({z}\right)=\:\frac{\mathrm{1}}{\left({z}^{\mathrm{2}\:} −{z}+\mathrm{1}\right)\left({z}^{\mathrm{2}} \:−\mathrm{2}{z}\:+\mathrm{4}\right)} \\ $$$${roots}\:{of}\:{z}^{\mathrm{2}} −{z}\:+\mathrm{1}\Rightarrow\Delta=\mathrm{1}−\mathrm{4}=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow{z}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:{and} \\ $$$${z}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}. \\ $$$${rootsof}\:{z}^{\mathrm{2}} \:−\mathrm{2}{z}\:+\mathrm{4}=\mathrm{0}\:\Rightarrow\Delta^{'} =\mathrm{1}−\mathrm{4}=−\mathrm{3}=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \Rightarrow \\ $$$$\alpha_{\mathrm{1}} =\mathrm{1}+{i}\sqrt{\mathrm{3}}\:\:{and}\:\:\alpha_{\mathrm{2}} =\mathrm{1}−{i}\sqrt{\mathrm{3}}\:\:{so} \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{z}−{z}_{\mathrm{1}} }\:+\frac{{b}}{{z}−{z}_{\mathrm{2}} }\:+\frac{{c}}{{z}−\alpha_{\mathrm{1}} }\:+\frac{{d}}{{z}−\alpha_{\mathrm{2}} }\:{let}\:{put}\: \\ $$$${p}\left({z}\right)=\left({z}^{\mathrm{2}\:} −{z}+\mathrm{1}\right)\left({z}^{\mathrm{2}} \:−\mathrm{2}{z}+\mathrm{4}\right)\:{tbe}\:{roots}\:{are}\:{simples}\:{so} \\ $$$${a}=\frac{\mathrm{1}}{{p}^{'} \left({z}_{\mathrm{1}} \right)}\bar {\:},\:{b}=\frac{\mathrm{1}}{{p}^{'} \left({z}_{\mathrm{2}} \right)}\:\:,\:{c}=\:\frac{\mathrm{1}}{{p}^{'} \left(\alpha_{\mathrm{1}} \right)}\:,\:{d}=\:\frac{\mathrm{1}}{{p}^{'} \left(\alpha_{\mathrm{2}} \right)}\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} {F}\left({z}\right){dz}={a}\int_{−\infty} ^{+\infty} \:\:\frac{{dz}}{{z}−{z}_{\mathrm{1}} }\:+{b}\int_{−\infty} ^{+\infty} \:\:\frac{{dz}}{{z}−{z}_{\mathrm{2}} }\:+{c}\int_{−\infty} ^{+\infty} \:\frac{{dz}}{{z}−\alpha_{\mathrm{1}} } \\ $$$$+\:\int_{−\infty} ^{+\infty} \:\:\frac{{dz}}{{z}−\alpha_{\mathrm{2}} }\:{but}\:{we}\:{have}\:{proved}\:{that} \\ $$$$\int_{{R}} \:\:\frac{{dz}}{{z}−{a}}={i}\pi\:{if}\:{Im}\left({a}\right)>\mathrm{0}\:{an}\overset{} {{d}}=−{i}\pi\:{if}\:{Im}\left({a}\right)<\mathrm{0}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{F}\left({z}\right){dz}=\frac{{i}\pi}{{p}^{'} \left({z}_{\mathrm{1}} \right)}\:−\frac{{i}\pi}{{p}^{'} \left({z}_{\mathrm{2}} \right)}\:+\frac{{i}\pi}{{p}^{'} \left(\alpha_{\mathrm{1}} \right)}\:−\frac{{i}\pi}{{p}^{'} \left(\alpha_{\mathrm{2}} \right)}\:{we}\:{have} \\ $$$${p}\left({z}\right)={z}^{\mathrm{4}} \:−\mathrm{2}{z}^{\mathrm{3}} \:+\mathrm{4}{z}^{\mathrm{2}} \:−{z}^{\mathrm{3}} \:+\mathrm{2}{z}^{\mathrm{2}} \:−\mathrm{4}{z}\:+{z}^{\mathrm{2}} \:−\mathrm{2}{z}\:+\mathrm{4} \\ $$$$={z}^{\mathrm{4}} \:−\mathrm{3}{z}^{\mathrm{3}} \:+\mathrm{7}{z}^{\mathrm{2}} \:−\mathrm{6}{z}\:+\mathrm{4}\:\Rightarrow{p}^{'} \left({z}\right)=\:\mathrm{4}{z}^{\mathrm{3}} \:−\mathrm{9}{z}^{\mathrm{2}} \:+\mathrm{14}{z}\:−\mathrm{6}\:{and} \\ $$$${the}\:{value}\:{of}\:{I}\:{is}\:{p}.{p}.{determined}.... \\ $$$$ \\ $$$$ \\ $$
