
Question Number 41846 by maxmathsup by imad last updated on 13/Aug/18
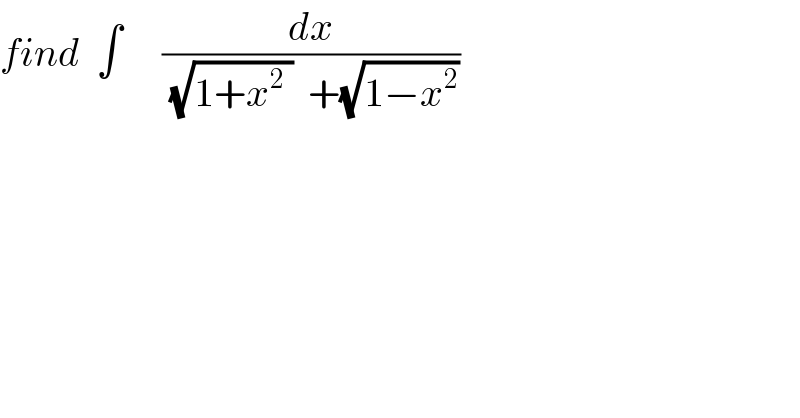
$${find}\:\:\int\:\:\:\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\:\:+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$
Answered by MJS last updated on 13/Aug/18
![∫(dx/((√(1+x^2 ))+(√(1−x^2 ))))=(1/2)∫((√(1+x^2 ))/x^2 )dx−(1/2)∫((√(1−x^2 ))/x^2 )dx= [both integrals by parts] =(1/2)(arcsin x +arcsinh x)+(((√(1−x^2 ))−(√(1+x^2 )))/(2x))+C](Q41850.png)
$$\int\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{both}\:\mathrm{integrals}\:\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{arcsin}\:{x}\:+\mathrm{arcsinh}\:{x}\right)+\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{2}{x}}+{C} \\ $$
Commented by math khazana by abdo last updated on 14/Aug/18

$${thank}\:{you}\:{sir}. \\ $$
