
Question Number 68033 by mathmax by abdo last updated on 03/Sep/19
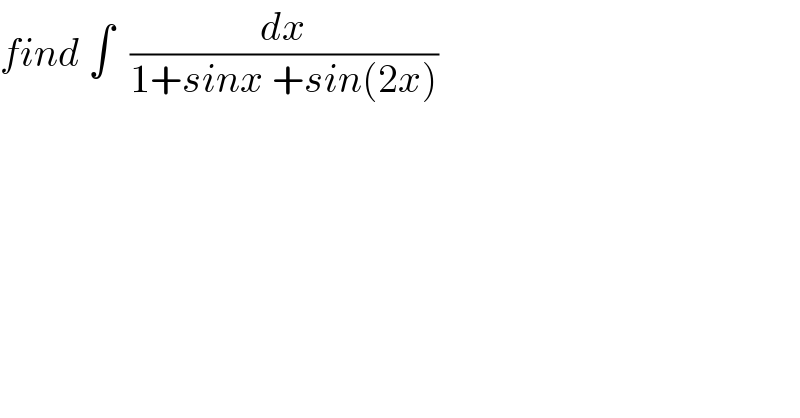
$${find}\:\int\:\:\frac{{dx}}{\mathrm{1}+{sinx}\:+{sin}\left(\mathrm{2}{x}\right)} \\ $$
Answered by MJS last updated on 04/Sep/19
![I think I did this before we have to use Weierstrass ∫(dx/(1+sin x +sin 2x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =2∫((t^2 +1)/((t+1)(t^3 −3t^2 +5t+1)))dt= =2∫((t^2 +1)/((t+1)(t−α)(t−β)(t−γ)))dt α=1+u+v β=1+(−(1/2)+((√3)/2)i)u−(−(1/2)−((√3)/2)i)v γ=1+(−(1/2)−((√3)/2)i)u−(−(1/2)+((√3)/2)i)v u=((−2+(2/9)(√(87))))^(1/3) v=((2+(2/9)(√(87))))^(1/3) now we have to decompose. the path is easy but the constants are terrible](Q68064.png)
$$\mathrm{I}\:\mathrm{think}\:\mathrm{I}\:\mathrm{did}\:\mathrm{this}\:\mathrm{before} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{use}\:\mathrm{Weierstrass} \\ $$$$\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}\:+\mathrm{sin}\:\mathrm{2}{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{5}{t}+\mathrm{1}\right)}{dt}= \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}−\alpha\right)\left({t}−\beta\right)\left({t}−\gamma\right)}{dt} \\ $$$$\alpha=\mathrm{1}+{u}+{v} \\ $$$$\beta=\mathrm{1}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}−\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$$$\gamma=\mathrm{1}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){u}−\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){v} \\ $$$${u}=\sqrt[{\mathrm{3}}]{−\mathrm{2}+\frac{\mathrm{2}}{\mathrm{9}}\sqrt{\mathrm{87}}} \\ $$$${v}=\sqrt[{\mathrm{3}}]{\mathrm{2}+\frac{\mathrm{2}}{\mathrm{9}}\sqrt{\mathrm{87}}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{decompose}.\:\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{easy} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{are}\:\mathrm{terrible} \\ $$
