
Question Number 67881 by mr W last updated on 01/Sep/19
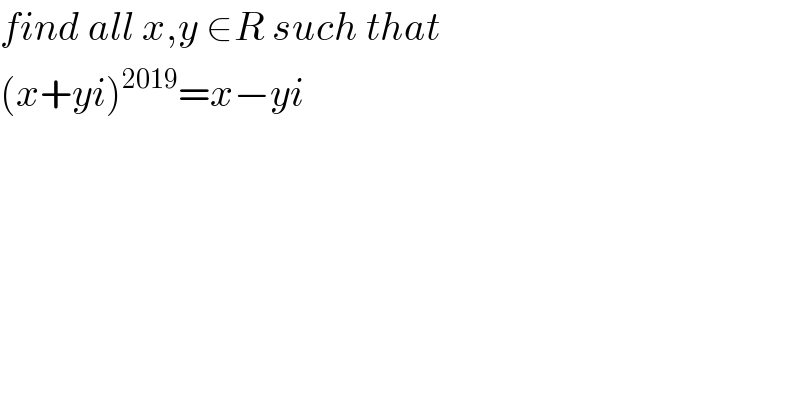
$${find}\:{all}\:{x},{y}\:\in{R}\:{such}\:{that} \\ $$$$\left({x}+{yi}\right)^{\mathrm{2019}} ={x}−{yi} \\ $$
Answered by mind is power last updated on 01/Sep/19
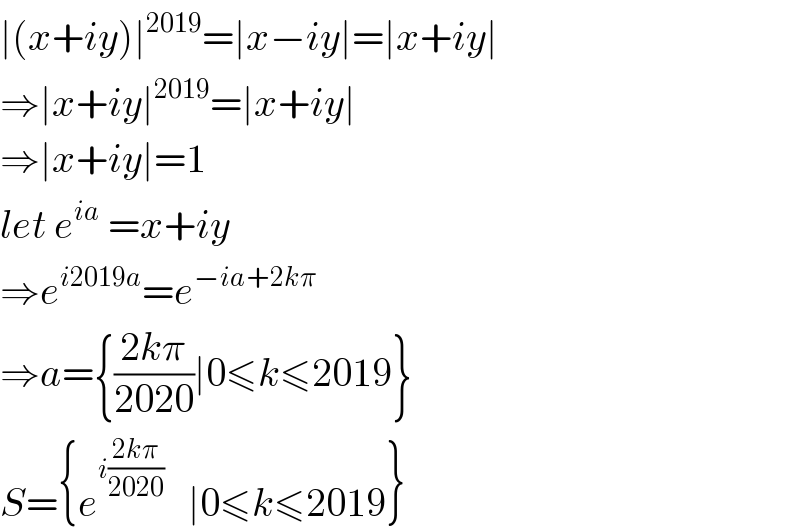
$$\mid\left({x}+{iy}\right)\mid^{\mathrm{2019}} =\mid{x}−{iy}\mid=\mid{x}+{iy}\mid \\ $$$$\Rightarrow\mid{x}+{iy}\mid^{\mathrm{2019}} =\mid{x}+{iy}\mid \\ $$$$\Rightarrow\mid{x}+{iy}\mid=\mathrm{1} \\ $$$${let}\:{e}^{{ia}} \:={x}+{iy} \\ $$$$\Rightarrow{e}^{{i}\mathrm{2019}{a}} ={e}^{−{ia}+\mathrm{2}{k}\pi} \\ $$$$\Rightarrow{a}=\left\{\frac{\mathrm{2}{k}\pi}{\mathrm{2020}}\mid\mathrm{0}\leqslant{k}\leqslant\mathrm{2019}\right\} \\ $$$${S}=\left\{{e}^{{i}\frac{\mathrm{2}{k}\pi}{\mathrm{2020}}} \:\:\:\mid\mathrm{0}\leqslant{k}\leqslant\mathrm{2019}\right\} \\ $$
Commented by mr W last updated on 01/Sep/19
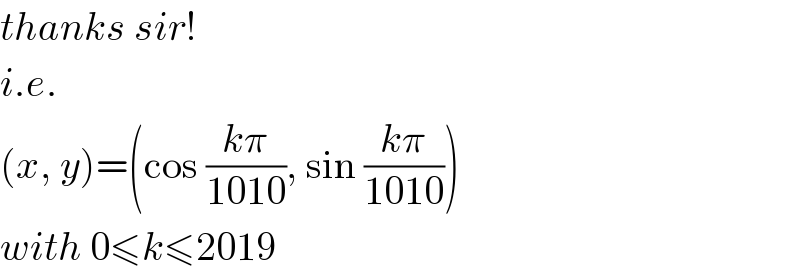
$${thanks}\:{sir}! \\ $$$${i}.{e}. \\ $$$$\left({x},\:{y}\right)=\left(\mathrm{cos}\:\frac{{k}\pi}{\mathrm{1010}},\:\mathrm{sin}\:\frac{{k}\pi}{\mathrm{1010}}\right) \\ $$$${with}\:\mathrm{0}\leqslant{k}\leqslant\mathrm{2019} \\ $$
Commented by mind is power last updated on 01/Sep/19

$${y}'{re}\:{welcom} \\ $$
