Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 211753 by alcohol last updated on 19/Sep/24

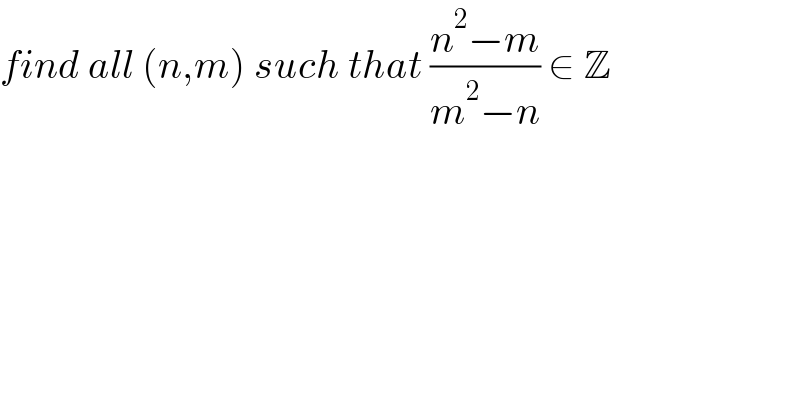
find all (n,m) such that ((n^2 −m)/(m^2 −n)) ∈ Z

$${find}\:{all}\:\left({n},{m}\right)\:{such}\:{that}\:\frac{{n}^{\mathrm{2}} −{m}}{{m}^{\mathrm{2}} −{n}}\:\in\:\mathbb{Z} \\ $$

Answered by Frix last updated on 20/Sep/24

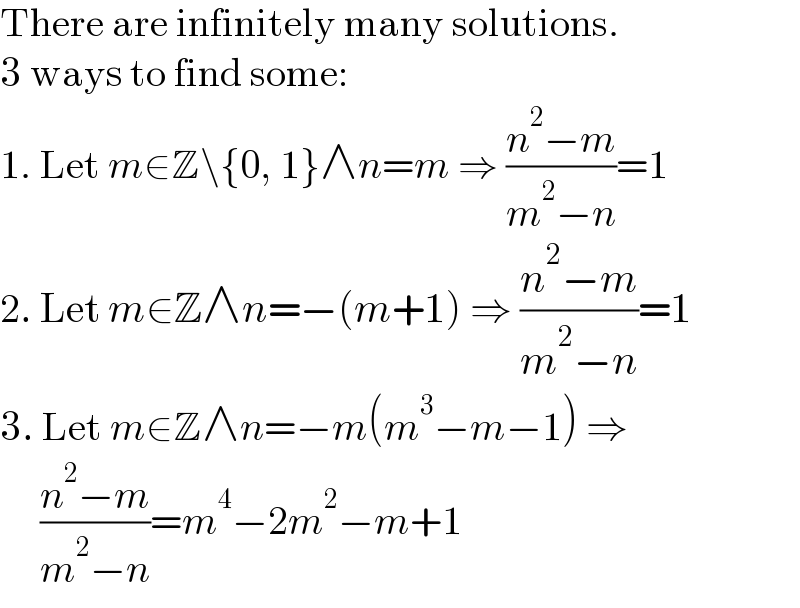
There are infinitely many solutions. 3 ways to find some: 1. Let m∈Z\{0, 1}∧n=m ⇒ ((n^2 −m)/(m^2 −n))=1 2. Let m∈Z∧n=−(m+1) ⇒ ((n^2 −m)/(m^2 −n))=1 3. Let m∈Z∧n=−m(m^3 −m−1) ⇒ ((n^2 −m)/(m^2 −n))=m^4 −2m^2 −m+1

$$\mathrm{There}\:\mathrm{are}\:\mathrm{infinitely}\:\mathrm{many}\:\mathrm{solutions}. \\ $$$$\mathrm{3}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{find}\:\mathrm{some}: \\ $$$$\mathrm{1}.\:\mathrm{Let}\:{m}\in\mathbb{Z}\backslash\left\{\mathrm{0},\:\mathrm{1}\right\}\wedge{n}={m}\:\Rightarrow\:\frac{{n}^{\mathrm{2}} −{m}}{{m}^{\mathrm{2}} −{n}}=\mathrm{1} \\ $$$$\mathrm{2}.\:\mathrm{Let}\:{m}\in\mathbb{Z}\wedge{n}=−\left({m}+\mathrm{1}\right)\:\Rightarrow\:\frac{{n}^{\mathrm{2}} −{m}}{{m}^{\mathrm{2}} −{n}}=\mathrm{1} \\ $$$$\mathrm{3}.\:\mathrm{Let}\:{m}\in\mathbb{Z}\wedge{n}=−{m}\left({m}^{\mathrm{3}} −{m}−\mathrm{1}\right)\:\Rightarrow \\ $$$$\:\:\:\:\:\frac{{n}^{\mathrm{2}} −{m}}{{m}^{\mathrm{2}} −{n}}={m}^{\mathrm{4}} −\mathrm{2}{m}^{\mathrm{2}} −{m}+\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com