
Previous in Relation and Functions Next in Relation and Functions
Question Number 90970 by abdomathmax last updated on 27/Apr/20
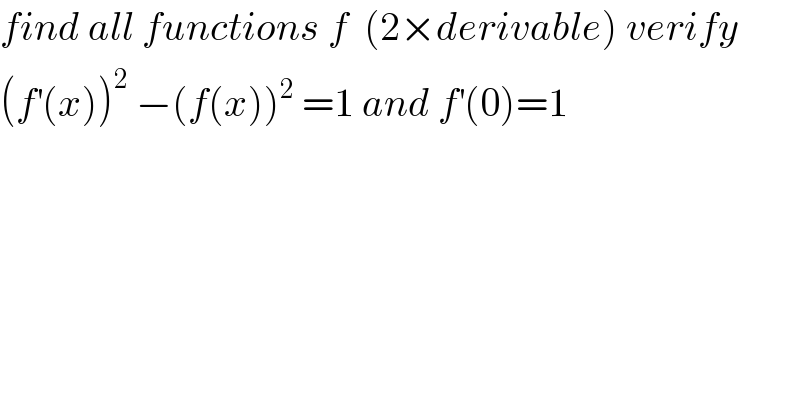
$${find}\:{all}\:{functions}\:{f}\:\:\left(\mathrm{2}×{derivable}\right)\:{verify} \\ $$$$\left({f}^{'} \left({x}\right)\right)^{\mathrm{2}} \:−\left({f}\left({x}\right)\right)^{\mathrm{2}} \:=\mathrm{1}\:{and}\:{f}^{'} \left(\mathrm{0}\right)=\mathrm{1} \\ $$
Commented by mr W last updated on 27/Apr/20
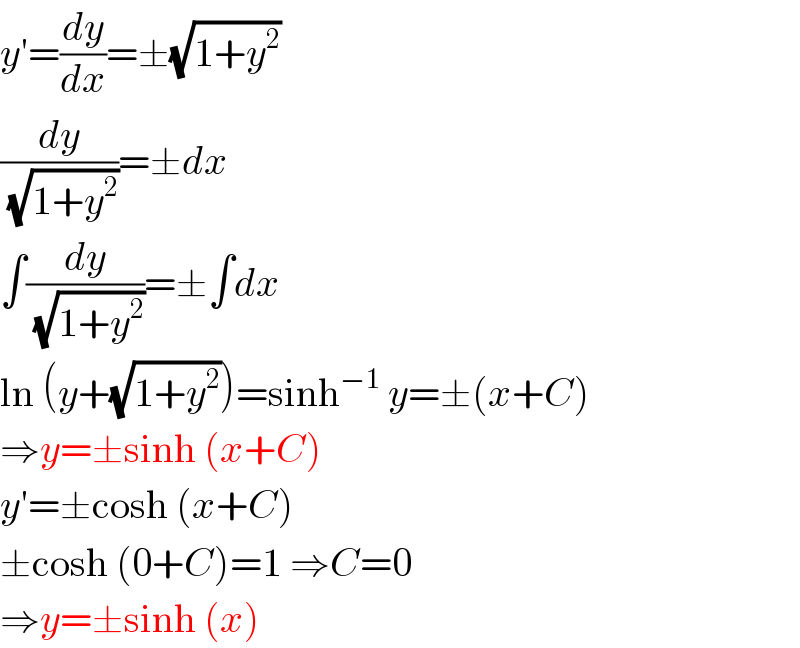
$${y}'=\frac{{dy}}{{dx}}=\pm\sqrt{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$$\frac{{dy}}{\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}=\pm{dx} \\ $$$$\int\frac{{dy}}{\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}=\pm\int{dx} \\ $$$$\mathrm{ln}\:\left({y}+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\right)=\mathrm{sinh}^{−\mathrm{1}} \:{y}=\pm\left({x}+{C}\right) \\ $$$$\Rightarrow{y}=\pm\mathrm{sinh}\:\left({x}+{C}\right) \\ $$$${y}'=\pm\mathrm{cosh}\:\left({x}+{C}\right) \\ $$$$\pm\mathrm{cosh}\:\left(\mathrm{0}+{C}\right)=\mathrm{1}\:\Rightarrow{C}=\mathrm{0} \\ $$$$\Rightarrow{y}=\pm\mathrm{sinh}\:\left({x}\right) \\ $$
Commented by mathmax by abdo last updated on 28/Apr/20

$${thank}\:{you}\:{sir}. \\ $$
