
Question Number 98673 by MJS last updated on 15/Jun/20
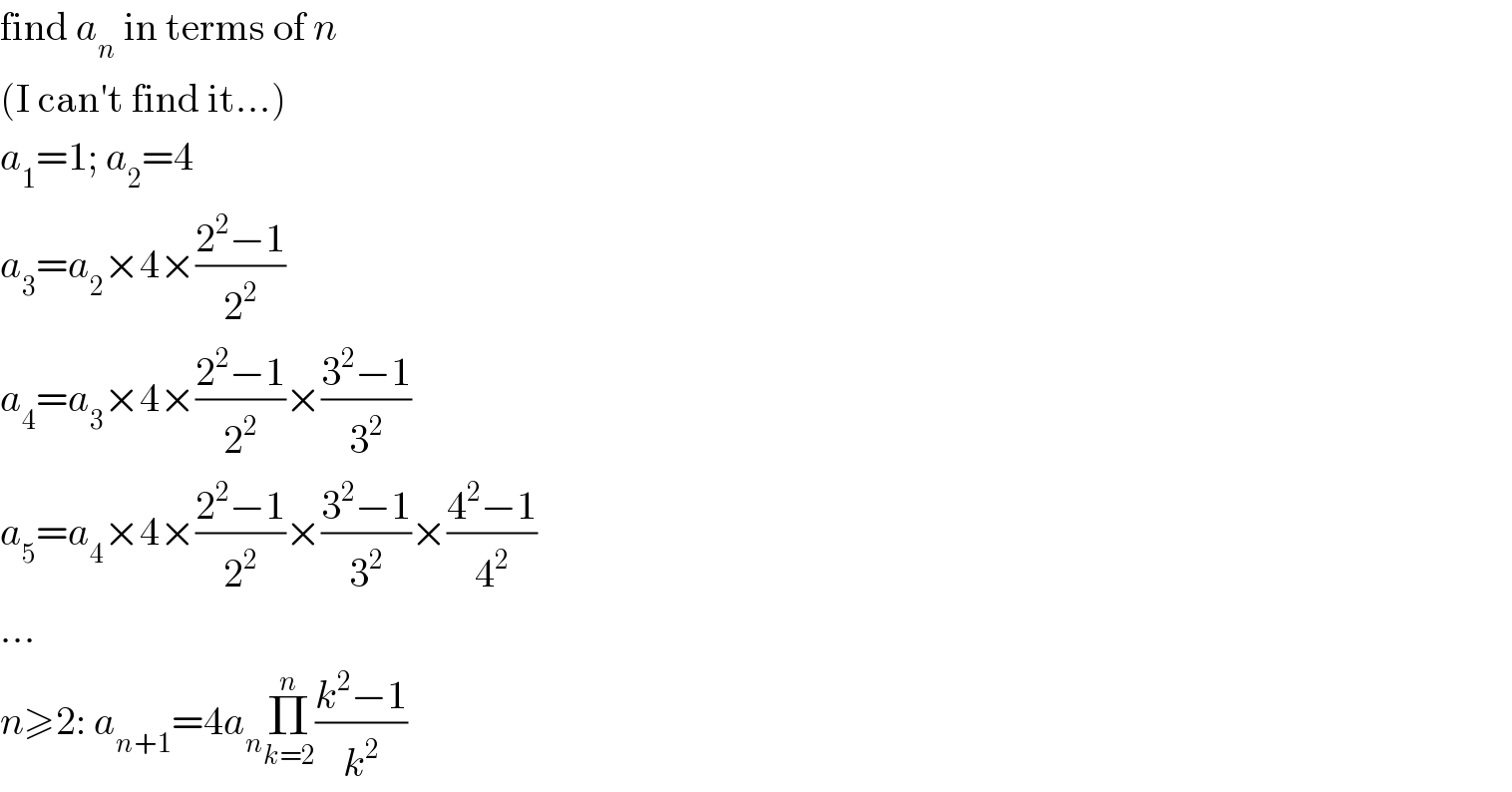
$$\mathrm{find}\:{a}_{{n}} \:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:{n} \\ $$$$\left(\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{find}\:\mathrm{it}...\right) \\ $$$${a}_{\mathrm{1}} =\mathrm{1};\:{a}_{\mathrm{2}} =\mathrm{4} \\ $$$${a}_{\mathrm{3}} ={a}_{\mathrm{2}} ×\mathrm{4}×\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}} } \\ $$$${a}_{\mathrm{4}} ={a}_{\mathrm{3}} ×\mathrm{4}×\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }×\frac{\mathrm{3}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}^{\mathrm{2}} } \\ $$$${a}_{\mathrm{5}} ={a}_{\mathrm{4}} ×\mathrm{4}×\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }×\frac{\mathrm{3}^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }×\frac{\mathrm{4}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}^{\mathrm{2}} } \\ $$$$... \\ $$$${n}\geqslant\mathrm{2}:\:{a}_{{n}+\mathrm{1}} =\mathrm{4}{a}_{{n}} \underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\frac{{k}^{\mathrm{2}} −\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$
Answered by M±th+et+s last updated on 16/Jun/20
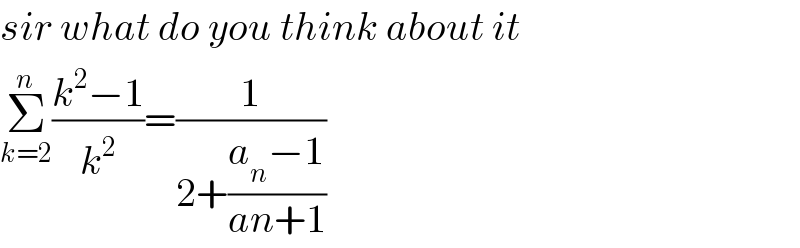
$${sir}\:{what}\:{do}\:{you}\:{think}\:{about}\:{it} \\ $$$$\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{2}} −\mathrm{1}}{{k}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}+\frac{{a}_{{n}} −\mathrm{1}}{{an}+\mathrm{1}}} \\ $$
Answered by maths mind last updated on 16/Jun/20
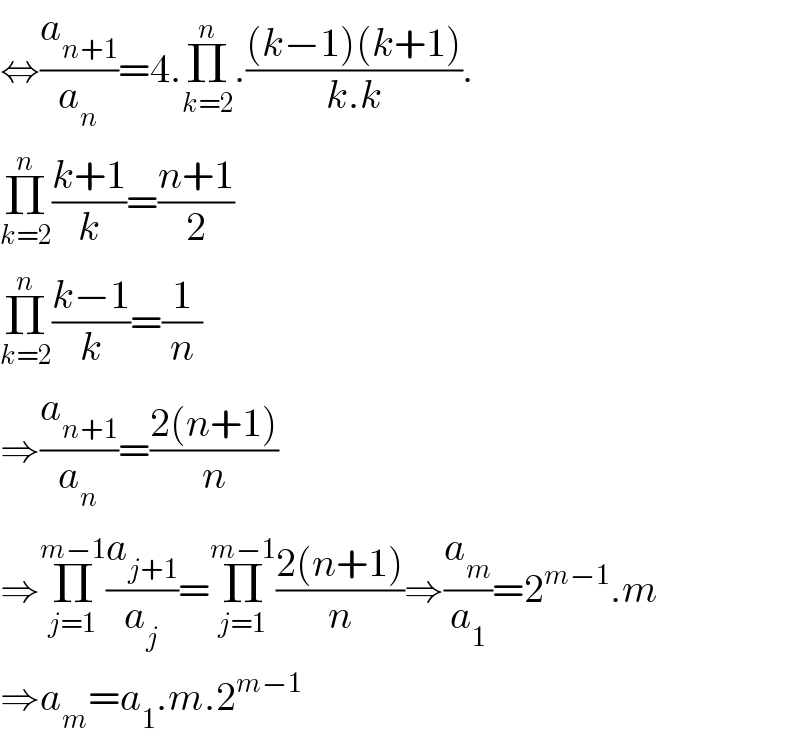
$$\Leftrightarrow\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }=\mathrm{4}.\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}.\frac{\left({k}−\mathrm{1}\right)\left({k}+\mathrm{1}\right)}{{k}.{k}}. \\ $$$$\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\frac{{k}+\mathrm{1}}{{k}}=\frac{{n}+\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\frac{{k}−\mathrm{1}}{{k}}=\frac{\mathrm{1}}{{n}} \\ $$$$\Rightarrow\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }=\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{{n}} \\ $$$$\Rightarrow\underset{{j}=\mathrm{1}} {\overset{{m}−\mathrm{1}} {\prod}}\frac{{a}_{{j}+\mathrm{1}} }{{a}_{{j}} }=\underset{{j}=\mathrm{1}} {\overset{{m}−\mathrm{1}} {\prod}}\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{{n}}\Rightarrow\frac{{a}_{{m}} }{{a}_{\mathrm{1}} }=\mathrm{2}^{{m}−\mathrm{1}} .{m} \\ $$$$\Rightarrow{a}_{{m}} ={a}_{\mathrm{1}} .{m}.\mathrm{2}^{{m}−\mathrm{1}} \\ $$
Commented by MJS last updated on 16/Jun/20
$$\mathrm{great},\:\mathrm{thank}\:\mathrm{you}!\:\mathrm{I}\:\mathrm{hadn}'\mathrm{t}\:\mathrm{thought}\:\mathrm{of}\:\mathrm{this} \\ $$
