Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 29455 by prof Abdo imad last updated on 08/Feb/18

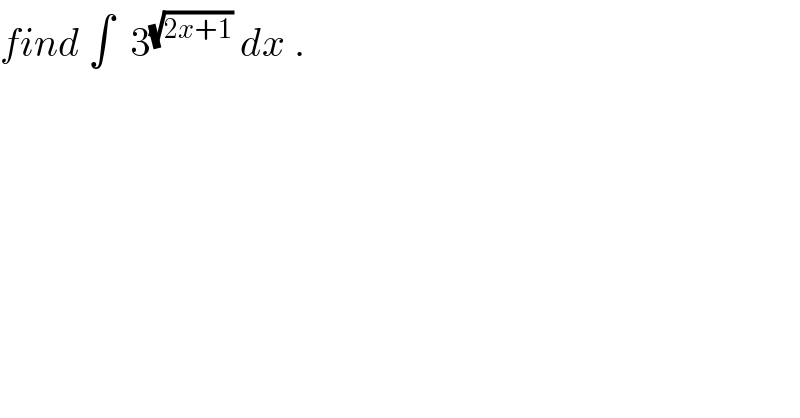
find ∫ 3^(√(2x+1)) dx .

$${find}\:\int\:\:\mathrm{3}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}} \:{dx}\:. \\ $$

Commented by prof Abdo imad last updated on 12/Feb/18

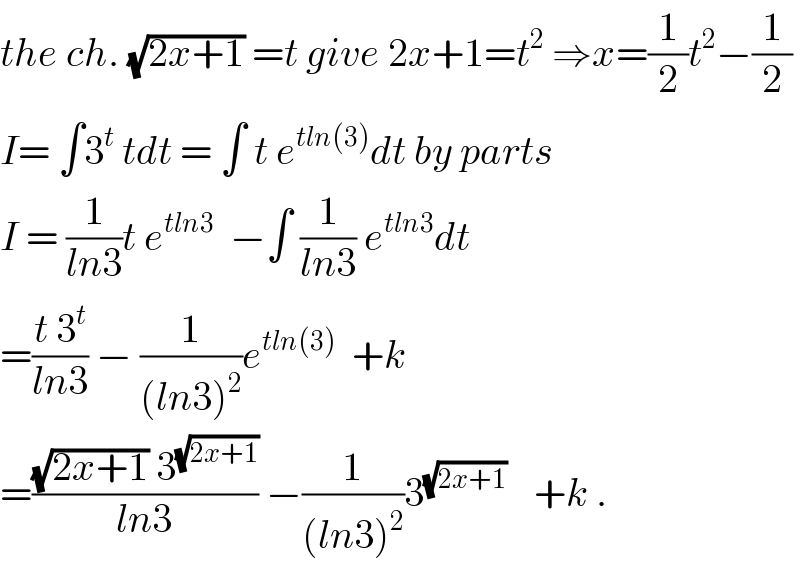
the ch. (√(2x+1)) =t give 2x+1=t^2 ⇒x=(1/2)t^2 −(1/2) I= ∫3^t tdt = ∫ t e^(tln(3)) dt by parts I = (1/(ln3))t e^(tln3) −∫ (1/(ln3)) e^(tln3) dt =((t 3^t )/(ln3)) − (1/((ln3)^2 ))e^(tln(3)) +k =(((√(2x+1)) 3^(√(2x+1)) )/(ln3)) −(1/((ln3)^2 ))3^((√(2x+1)) ) +k .

$${the}\:{ch}.\:\sqrt{\mathrm{2}{x}+\mathrm{1}}\:={t}\:{give}\:\mathrm{2}{x}+\mathrm{1}={t}^{\mathrm{2}} \:\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${I}=\:\int\mathrm{3}^{{t}} \:{tdt}\:=\:\int\:{t}\:{e}^{{tln}\left(\mathrm{3}\right)} {dt}\:{by}\:{parts} \\ $$$${I}\:=\:\frac{\mathrm{1}}{{ln}\mathrm{3}}{t}\:{e}^{{tln}\mathrm{3}} \:\:−\int\:\frac{\mathrm{1}}{{ln}\mathrm{3}}\:{e}^{{tln}\mathrm{3}} {dt} \\ $$$$=\frac{{t}\:\mathrm{3}^{{t}} }{{ln}\mathrm{3}}\:−\:\frac{\mathrm{1}}{\left({ln}\mathrm{3}\right)^{\mathrm{2}} }{e}^{{tln}\left(\mathrm{3}\right)} \:\:+{k} \\ $$$$=\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}\:\mathrm{3}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}} }{{ln}\mathrm{3}}\:−\frac{\mathrm{1}}{\left({ln}\mathrm{3}\right)^{\mathrm{2}} }\mathrm{3}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}\:} \:\:\:+{k}\:. \\ $$

Answered by sma3l2996 last updated on 09/Feb/18

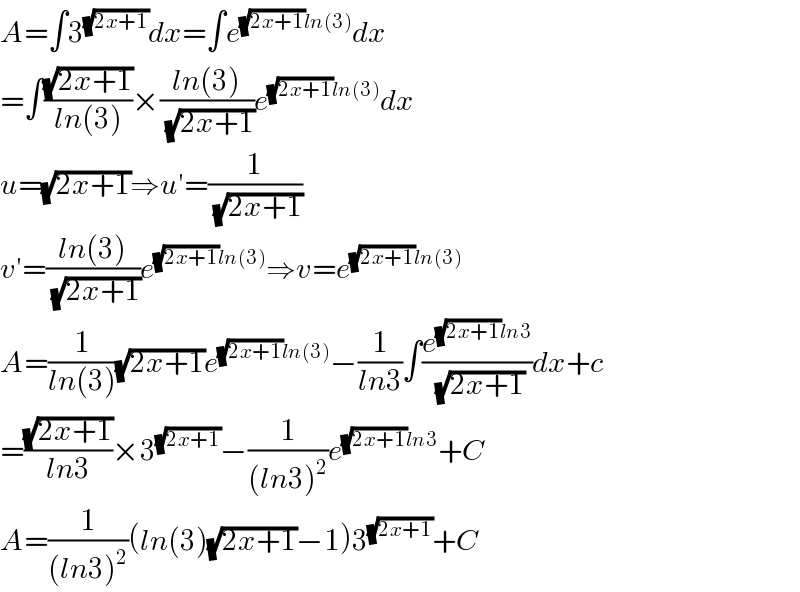
A=∫3^(√(2x+1)) dx=∫e^((√(2x+1))ln(3)) dx =∫((√(2x+1))/(ln(3)))×((ln(3))/(√(2x+1)))e^((√(2x+1))ln(3)) dx u=(√(2x+1))⇒u′=(1/(√(2x+1))) v′=((ln(3))/(√(2x+1)))e^((√(2x+1))ln(3)) ⇒v=e^((√(2x+1))ln(3)) A=(1/(ln(3)))(√(2x+1))e^((√(2x+1))ln(3)) −(1/(ln3))∫(e^((√(2x+1))ln3) /(√(2x+1)))dx+c =((√(2x+1))/(ln3))×3^(√(2x+1)) −(1/((ln3)^2 ))e^((√(2x+1))ln3) +C A=(1/((ln3)^2 ))(ln(3)(√(2x+1))−1)3^(√(2x+1)) +C

$${A}=\int\mathrm{3}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}} {dx}=\int{e}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}{ln}\left(\mathrm{3}\right)} {dx} \\ $$$$=\int\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{{ln}\left(\mathrm{3}\right)}×\frac{{ln}\left(\mathrm{3}\right)}{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{e}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}{ln}\left(\mathrm{3}\right)} {dx} \\ $$$${u}=\sqrt{\mathrm{2}{x}+\mathrm{1}}\Rightarrow{u}'=\frac{\mathrm{1}}{\sqrt{\mathrm{2}{x}+\mathrm{1}}} \\ $$$${v}'=\frac{{ln}\left(\mathrm{3}\right)}{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{e}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}{ln}\left(\mathrm{3}\right)} \Rightarrow{v}={e}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}{ln}\left(\mathrm{3}\right)} \\ $$$${A}=\frac{\mathrm{1}}{{ln}\left(\mathrm{3}\right)}\sqrt{\mathrm{2}{x}+\mathrm{1}}{e}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}{ln}\left(\mathrm{3}\right)} −\frac{\mathrm{1}}{{ln}\mathrm{3}}\int\frac{{e}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}{ln}\mathrm{3}} }{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{dx}+{c} \\ $$$$=\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{{ln}\mathrm{3}}×\mathrm{3}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}} −\frac{\mathrm{1}}{\left({ln}\mathrm{3}\right)^{\mathrm{2}} }{e}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}{ln}\mathrm{3}} +{C} \\ $$$${A}=\frac{\mathrm{1}}{\left({ln}\mathrm{3}\right)^{\mathrm{2}} }\left({ln}\left(\mathrm{3}\right)\sqrt{\mathrm{2}{x}+\mathrm{1}}−\mathrm{1}\right)\mathrm{3}^{\sqrt{\mathrm{2}{x}+\mathrm{1}}} +{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com