
Question Number 203884 by Mathspace last updated on 31/Jan/24
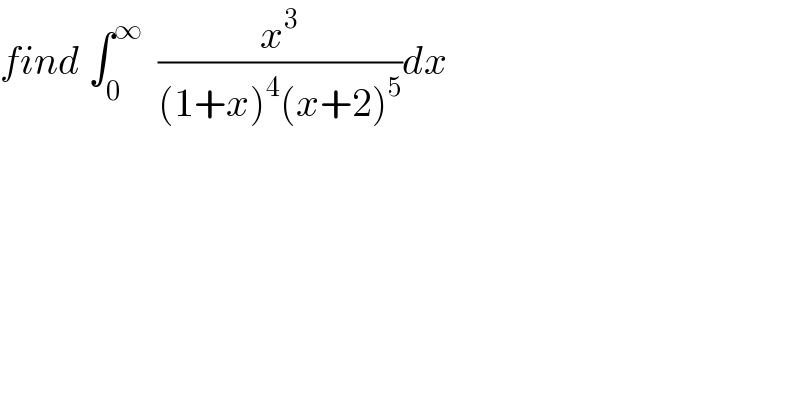
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{3}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{4}} \left({x}+\mathrm{2}\right)^{\mathrm{5}} }{dx} \\ $$
Answered by Frix last updated on 01/Feb/24
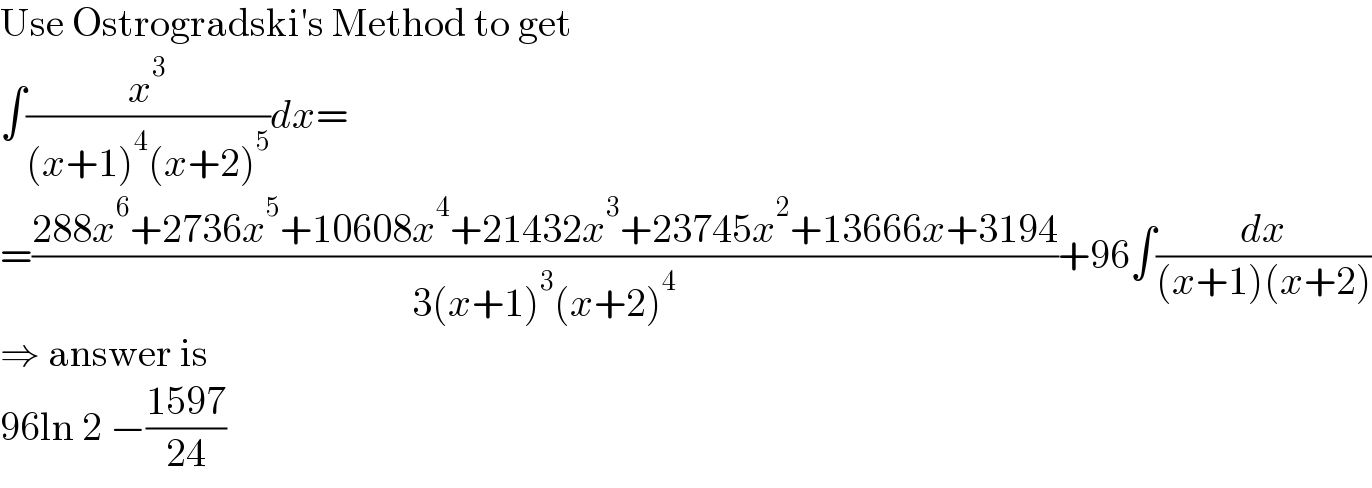
$$\mathrm{Use}\:\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\:\mathrm{to}\:\mathrm{get} \\ $$$$\int\frac{{x}^{\mathrm{3}} }{\left({x}+\mathrm{1}\right)^{\mathrm{4}} \left({x}+\mathrm{2}\right)^{\mathrm{5}} }{dx}= \\ $$$$=\frac{\mathrm{288}{x}^{\mathrm{6}} +\mathrm{2736}{x}^{\mathrm{5}} +\mathrm{10608}{x}^{\mathrm{4}} +\mathrm{21432}{x}^{\mathrm{3}} +\mathrm{23745}{x}^{\mathrm{2}} +\mathrm{13666}{x}+\mathrm{3194}}{\mathrm{3}\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{4}} }+\mathrm{96}\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is} \\ $$$$\mathrm{96ln}\:\mathrm{2}\:−\frac{\mathrm{1597}}{\mathrm{24}} \\ $$
